SymForce 란?

• 최근 RSS 2022 에서 SymForce 라는 framework 이 공개되었다. Skydio 가 공개하였다. 내부적으로 5년동안 개발하고 실제로 사용해온 것이라고 한다.
• Skydio 는 초기에 GTSAM 저자이신 + SLAM 역사에 큰 획을 그은 Frank Dellaert 교수님의 자문을 받았다고 들었다. 최근에는 멋진 결과들도 보여주고 있어서, 이들의 기술력은 어떤 수준일지 궁금했었다.
• SymForce 논문을 보면 robotics (특히 드론 등)와 같이 빠른 계산이 실시간으로 요구될 때에는, (Ceres 같은) 계산그래프 기반보다 symbolic 기반 의 미분이 더 좋다고 주장하고 있다. 원래 Robotics 에서 Ceres 가 많이 쓰이고 있어서 새로운 solver 의 필요성을 못 느끼고 있었는데, 이 논문의 말을 들어보면 왠지 설득이 된다.
• 한 번 공부할겸 써보았다.

Nonlinear ICP 구현하기

목표

• Nonlinear ICP 를 구현해보자.

배경지식

Nonlinear optimization

• Nonlinear optimization 어쩌구 하면 == Gauss-Newton으로 iterative 하게 푼다 라고 이해해도 거의 무방하다.
• 이 때 update step 의 방향과 크기를 계산하기 위해 cost function 의 미분값이 필요하고 이것을 Jacobian이라고 부른다.
  • 이 때 cost function output dimension 이 $n$이고, cost function 을 구성하는 우리가 찾고싶은 최적값에 대한 파라미터 변수의 dimension 이 $m$이라고 하면 Jacobian의 shape 은 $n \times m$이 되게 된다.

Auto diff

• 그런데 nonlinear한(즉 $a_0 x_0 + a_1 x_ 1 + …$ 형태가 아닌 모든 포맷) 복잡한 cost function 의 Jacobian 을 사람이 손으로 계산하는 것은 실수할 위험이 크기 때문에, 변수들을 계산그래프로 연결하고, 자동으로 미분값이 관리되도록 (전파되도록) 하는 구현을 채택하는 방식이 널리 쓰이고 있다 (e.g., Ceres, Pytorch)
  • 이 경우, forward 전파될 때 하나의 변수에 대해 value와 gradient 의 두 값을 동시에 함께 저장해야 되게된다. 예를 들어, Ceres 에서는 jet이라는 형태로 관리되고, autodiff 에서는 dual 이라는 이름이 쓰이고 있다.

Symbolic diff

• 이렇게 jet, dual 등의 구조체로 두 값을 관리하면서 계산그래프를 형성하는 식의 autodiff 가 robotics 와 deep learning 분야 모두에 대해서 널리 쓰이고 있는 (Ceres, autodiff, tinyAD, jax, pytorch, tensorflow 등등등) 요즘이지만 …
• SymForce 는 Symbolic 기반이라고 한다. 즉, 임의의 cost function 이 주어질 때, 이것의 자코비안을 명시적으로 식으로 딱 계산해준다. 그리고 이 계산이 최적화되도록 해준다.
  • 그리고 python 으로 수식을 적으면 c++ code 를 생성해주기까지 한다!
• 예를 들어, ICP에서 cost function 은 다음과 같다. 3D point $p_0$ 과 point $p_1$이 주어질 때, loss $= ||\left( R \{ \theta \}*p_0 + t \right) - p_1 || _2$ 를 최소화하는 transformation parameter $\theta$ 와 $t$ 를 찾는 것이 목표이다.
  • 이 때 자연스럽게 그러면 다음과 같은 질문(멘붕)에 빠지게 된다. $\frac{\partial\text{loss}}{\partial\bf{\theta}}$ 와 $\frac{\partial\text{loss}}{\partial{t}}$를 어떻게 계산하지 ..???!?
  • 이 때 이걸 계산그래프로 묶어서 값을 주면 autodiff 이고.. 명시적으로 (수작업 기준)복잡한 수식을 찾아주는 게 symbolic 이라고 일단 이해하고 있다 (더 공부 필요)
  • 즉, SymForce 에게 이 작업을 맡기면 $\frac{\partial\text{loss}}{\partial\bf{\theta}}$이 다음과 같이 아래 그림처럼 나온다 (너무 길어서 다 옮길 수가 없어서 캡처로 대신한다. 전체 식은 여기 jupyter notebook를 참고).

    

  • 이 때 $\theta$는 rotation 을 minimal 하게 parametrize 하는 angle-axis 가 된다. 이를 tangent space 에서 최적화한다라고도 표현하고, 이후에 이 값을 원래 공간 (e.g., rotation에 대해서는 $\text{SO(3)}$) 으로 보내주는 작업을 retract 라고 부르기도 하고 … 이에 대해서는 별도의 rotation 관련 자료(A micro Lie theory for state estimation in robotics, Quaternion kinematics for the error-state Kalman filter )를 참고하도록 하자.
• 아무튼 요약하자면 Jacobain matrix 의 값을 알면 iterative update 하는 것은 너무 쉬운데, 이 때 아무리 복잡한 함수여도 SymForce 가 자코비안을 알아서 잘 구해준다는 것. 특히 robotics 에서 많이 사용하는 parameter 들 (camera projection, rotation 등) 에 대한 지원을 포함하고 있기 때문에 SymPy 등의 기존 Symbolic solver 들을 사용할 때보다 robotics 문제를 더 풀기 편리해졌다는 점 등이 장점이라고 할 수 있겠다.

구현

Iterative update

• 자코비안을 구한다음, 이것을 이용해서 iterative 하게 최적의 $d[\theta, t]$ 를 구하고, 조금씩 이 값을 업데이트 해나가는 루틴은 너무나 자명하다. 이에 대해서는 Grisetti 교수님의 2016년 ICRA tutorial 자료 를 추천한다. 여기에 보면 이런 식이 있다. Octave (Matlab) 구현체이다.

• 위의 구조를 python으로 옮기면 다음과 같이 된다. (전체 코드는 여기 symforce-tutorials 서 볼 수 있다).

  def icp(src, tgt, tf_init, max_iter=5, verbose=False):
  
    tf = tf_init # 6 dim
    num_pts = src.shape[0]
  
    for _iter in range(max_iter):
        # reset for each iter
        H = np.zeros((6, 6))
        b = np.zeros((6, 1))
  
        # gathering measurements
        for pt_idx in range(num_pts):
  
            src_pt = src[pt_idx, :]
            tgt_pt = tgt[pt_idx, :]
  
            e, Je_rot, Je_trans \
                = evaluate_error_and_jacobian(src_pt, tgt_pt, tf)
  
            J = np.hstack((Je_rot, Je_trans)) # thus, 3x6
  
            H = H + J.T @ J # H: 6x3 * 3x6 => thus H is 6x6
            b = b + J.T @ e # b: 6x3 * 3x1 => thus b is 6x1
  
        dtf = -np.linalg.solve(H, b).squeeze() # note the step direction is minus
        tf = tf + dtf # updated within the tangent space
  
    return tf
  

  • note: 이 때 src_pt와 tgt_pt 는 실제로 같은 지점의 포인트여야 한다. 즉, correspondence 여야 한다.
    • ps. 이번 튜토리얼은 교육용으로 작성해본 것 (1. SymForce를 이용해서 자동으로 Jacobian을 심볼릭 기반으로 계산해보기 2. 이를 이용해서 nonlinear optimization 의 update 부분 from scratch로 구현해보기) 이기 때문에… point cloud $\text{pcd}_0$(위의 리포에서 data/251371071.pcd를 로드하고 임의의 $\text{SE(3)}$ transformation 을 가해주어서 $\text{pcd}_1$ 을 생성하고 있다. 따라서 point 의 순서가 보존되므로 src_pt와 tgt_pt 모두 동일한 인덱스 pt_idx 로 가져오면 correspondence 가 성립된다. 실제 세계 문제에서는 FPFH local feature 등의 방법으로 correspondence 를 먼저 찾고, 잘 associate 된 pair 를 위의 icp 알고리즘에 넣어주어야 한다.
  • 위의 루틴은 특별히 어려울 것은 없다. Robotics 문제에서 ICP뿐 아니라 어떤 알고리즘이 되더라도 결국 위의 모습을 하게 된다.
  • 이 때 그러면 위의 루틴에서 Jacobian을 계산해주는 evaluate_error_and_jacobian 함수를 디자인하는 것이 로보틱스 엔지니어의 역할이 된다. 그런데 그것을 이제 SymForce가 수행해준다. 아래 코드처럼 정의된 모델에 해당 데이터포인트에서의 값을 넣어주기만 하면된다. 이 역할을 하는 것이 SymForce 에서 .subs method 인데 substitution 을 의미한다.

      def evaluate_error_and_jacobian(src_pt: np.ndarray, tag_pt: np.ndarray, transformation):
      # note: transformation is 6dim vector on the tangent space (i.e., [rotvec, trans])
    
          def inject_values(model):
              model_evaluated = \
                  model.subs(rotvec, sf.V3(transformation[:3])) \
                       .subs(transvec, sf.V3(transformation[3:])) \
                       .subs(p_src, sf.V3(src_pt)) \
                       .subs(p_tgt, sf.V3(tag_pt))
              return model_evaluated
    
          error = inject_values(error_model)
          Je_rot = inject_values(Je_rot_model)
          Je_trans = inject_values(Je_trans_model)
    
      return error.to_numpy(), Je_rot.to_numpy(), Je_trans.to_numpy()
    

  • 참고로 여기에 쓰이는 error_model, Je_rot_model, Je_trans_model 등은 아래 코드와 같이 편하게 생성할 수 있다.

      # Model parameters (as symbolic)
      transvec = sf.V3.symbolic("t")
      rotvec   = sf.V3.symbolic("Theta") # i.e., angle-axis parametrization
      rotmat   = LieGroupOps.from_tangent(sf.Rot3, rotvec) # for debug, display(rotmat.to_rotation_matrix())
    
      # Redisual (loss function)
      #  note: the rotation 'matrix' is used to formulate the below constraint,
      #        but it was parametrized as a 3-dim vector 'rotvec'!
      p_src        = sf.V3.symbolic("p_src")     # p means a single 3D point
      p_tgt        = sf.V3.symbolic("p_tgt")
      p_tgt_est    = (rotmat * p_src) + transvec # The constraint: R*p + t == p'
    
      error_val = p_tgt_est - p_tgt
    
      def loss(error_V3):
          for i in range(3):
              error_V3[i] = sf.sqrt(error_V3[i]*error_V3[i])
          return error_V3
    
      error_model = loss(error_val)
    
      # residual jacobian
      #  this is the powerful moment of symforce. It automatically generate the Jacobian equations explicitly.
      Je_trans_model = error_model.jacobian(transvec)
      Je_rot_model = error_model.jacobian(rotvec)
    

    • V3등은 3 dimension vector 를 의미한다. 이렇듯 SymForce 에서 지원하는 symbolic class 로 변수를 잘 이어붙여서 error function 을 정의해주고, 여기에 .jacobian(w.r.t what) 라고만 해주면 준비 끝.
      • ps. 여기서 rotvec, rotmat 등의 차이에 대해 배경지식을 구비하기 위해서는 앞서도 이야기했지만 rotation 관련 자료(A micro Lie theory for state estimation in robotics, Quaternion kinematics for the error-state Kalman filter)를 참고하도록 하자.

결과

• 그래서 icp 함수를 수행하면, 다음 결과(캡처)와 같이 임의로 처음에 가했던 transformation과 최적화해서 찾은 예측값이 동일함을 알 수 있다.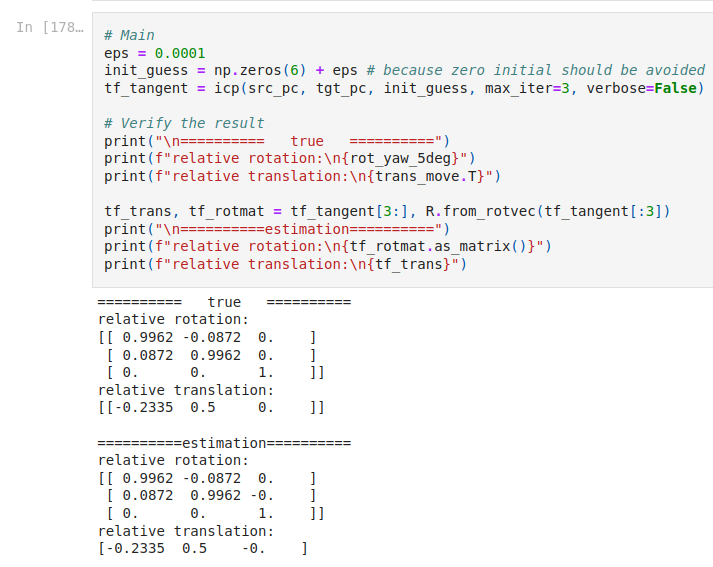

  

  • diff_SE3 값을 달리해가면서 체험해보길 바란다! 그래도 늘 같은 값을 잘 예측하는 것을 알 수 있다.
    • 여기 유튜브 영상에서 수렴과정을 시각화하였다.

결론

요약

1. SymForce 는 로보틱스 문제를 풀 때 필요한 자코비안을 잘 생성해준다.
2. Gauss-Newton pipeline 을 구성해볼 때 가장 애먹는 부분이 Jacobian 을 구하는 부분인데, 이 부분을 캡슐화하고 나니, nonliear update pipeline 을 구현하는 데 좀 더 집중하여 최적화 과정을 더 잘 파악해볼 수 있다.
   • 전체 코드는 여기 (link) 서 볼 수 있다
   • ps. 복잡한 nonlinear cost 의 Jacobian 구하는 것부터 신경쓰게 되는 것은 입문자 입장에서 (수학적으로) 어렵다. 그렇다고 이를 회피하다 보면, 매번 너무 쉬운 예제만을 다루게 된다. 즉 로보틱스 실전 문제 중 항상 일부만 다루게 되거나 2D space 에 한정되므로 아쉽다.. (e.g., 2D에서의 differential wheel motion 등).

TODO

• 공부삼아 Gauss-Newton update 과정을 구성해보았지만, 아마 optimizer 라는 class 로 이런 과정들이 이미 wrapping 되어있는 듯 하다. SymForce 가 제공하는 조금 더 high-level에서의 optim API를 사용해보자
• Cauchy kernel 을 씌워서 loss function 을 from scratch로 구현해보자. 그리고 noisy 한 correspondences pairs 가 주어졌을 때 robust kernel 여부에 따른 강건성 차이를 실습해보자. 그리고 GncOptimizer도 사용해보자.
• Automatically generated C++ code 기준 Ceres 와의 속도차이를 실제로 테스트해보자.