Illustrated Fast Kalman Gain Computation
- Kalman Gain 계산에는 matrix inversion 이 포함되어 있다.
- 근데 Matrix inversion 은 비싸다.
- FAST-LIO의 K 계산 과정에서의 Matrix 모양을 그림으로 그려서 알아보자.
대상독자
속도를 빠르게 하려면?
일반적으로
- 모든 geometric optimization 은 두 단계로 나뉜다고 할 수 있다.
- Problem buildling
- Problem solving
- Proboem building 은 correspondences를 찾고 constraints 를 만드는 과정, Problem solving 은 그 constraints 를 모두 (거의) 만족하는 optimal solution을 찾는 과정을 의미한다.
- 예를 들어 통상적인 least square optimization 에서
- $A\delta x=b$ 를 Gauss-newton 으로 푸는 것이 solving 과정이고,
- 이를 위한 $A$ matrix 자체를 만드는 일 (및 그것을 위한 모든 앞단: e.g., 이미지 전처리, 특징점 검출, 피처 추출 등)이 problem building 이라고 할 수 있을 것이다.
- 예를 들어 통상적인 least square optimization 에서
SLAM에서
- FAST-LIO와 같은 LiDAR(or visual)-SLAM에서는
- map 의 entity와 query measurement 의 entity 사이의 correspondence 를 찾는 것이 buildilng,
- 그 사이의 residual 을 최소화하는 solution을 찾는 과정이 solving 이라고 할 수 있겠다.
FAST-LIO에서
- FAST-LIO에서는 그래서 크게 contribution이 두 가지라고 할 수 있다.
- Geometric optimization 의 두 단계에 대하여 각각 시간개선을 위한 contributions이 있었다.
- ikd-tree 를 통한 problem buildling 시간 개선
- 즉, map 관리를 더 빠르게 할 수 있고, map으로 부터 correspondence 를 더 빨리 retrieval 해올 수 있게 되었다.
- ps. 이후 faster-lio 나 voxel-map 에서는 kd-tree 보다도 근본적으로 빠른 hash map을 제안하기도 하였다. 아무튼 이런 노력들은 모두 problem buildling 시간 단축에 기여하는 요소라고 할 수 있다.
- 즉, map 관리를 더 빠르게 할 수 있고, map으로 부터 correspondence 를 더 빨리 retrieval 해올 수 있게 되었다.
- Fast Kalman Gain computation 을 통한 problem solving 시간 개선
- 이 부분에 대해서 이 포스트에서 자세하게 설명해보고자 한다.
- ikd-tree 를 통한 problem buildling 시간 개선
- Geometric optimization 의 두 단계에 대하여 각각 시간개선을 위한 contributions이 있었다.
The Fast Kalman Gain
- 구글에서 Kalman Gain 이라고 검색해보면 (혹은 이 자료 (2006 An Introduction to the Kalman Filter)를 보라), 통상적인 Kalman Gain 은 이렇게 생겼다.
- Slow K: $ \textbf{K} = \textbf{P}\textbf{H}^{\textbf{T}}(\textbf{H}\textbf{P}\textbf{H}^{T} + \textbf{R})^{-1}$
- 그런데 FAST-LIO에서 사용하는 Kalman Gain은 이렇게 생겼다.
- Fast K: $ \textbf{K} = (\textbf{H}^{T}\textbf{R}^{-1}\textbf{H}+\textbf{P}^{-1})^{-1}\textbf{H}^{T}\textbf{R}^{-1}$
- 전자를 slow K, 후자를 fast K 라고 부르자.
- FAST-LIO 논문에 의하면 아래 유도과정에 의해 fast ver와 slow ver 는 동치라고 한다.

- The slow version 으로 불리는 $\textbf{K}$는 Conventional 한 Kalman filter 의 Gain form 으로 아주 잘 알려진 형태인데, 그렇다면 지금까지 문제가 많았단걸까? 그게 아니라면, 왜 slow version $\textbf{K}$는 특히 FAST-LIO에서 slow 할 수밖에 없었을까? 왜 그럴지 알아보자.
Matrix-illustrated Fast Kalman Gain
- Kalman gain 의 식에 있는 $\textbf{H}$는 residual 의 미분값 (jacobian) 이다. 예를 들어, visual SLAM에서, image feature 에 대해서는 reprojection error 를 주로 많이 사용한다. r2live 의 논문 appendix 에 이 식이 잘 나와있다 (eq S7 참고).
- 하나의 residual 에 대한 $\textbf{H}$ (그래서 constraint $i$에 대한 residual 이라고 해서 $\textbf{H}_i$ 와 같이 쓸 수도 있겠고)는 항상 이런 모양이다.
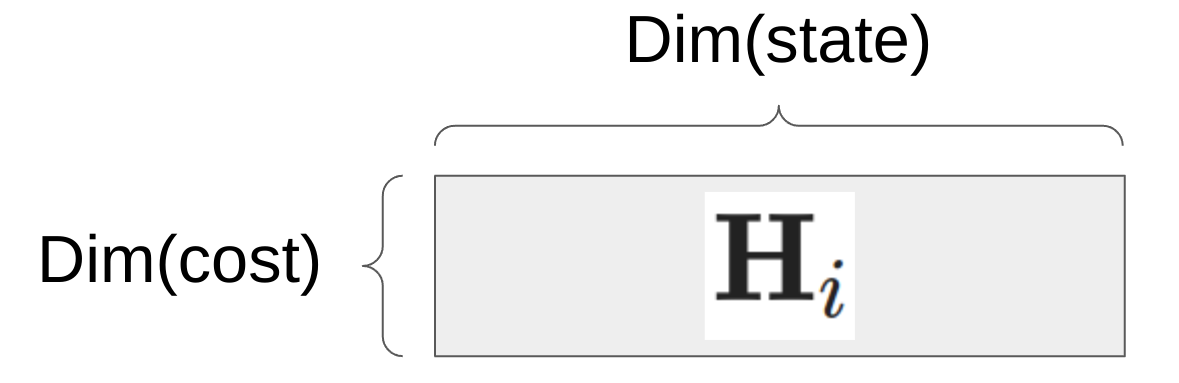
- cost (or called error, residual) 는 정의하기 나름이다. image 의 feature point reprojection error 는 보통 x로의 diff와 y로의 offset 을 모두 측정하므로 Dim(cost)=2 가 되겠다 (r2live 의 논문 appendix 에 이 식이 잘 나와있다 (eq S7, S10 참고).
- 한 편, Dim(state)는 우리가 알고싶은 robot 의 상태변수를 의미한다. 아주 일반적으로는 rotation 과 translation 이므로 =6 이라고 할 수 있겠다.
- rotation은 error-state 의 경우 minimal representation (i.e., tangent vector space) 로 표현되므로 rotation 의 dimension=3, translation의 dimension=3 (xyz) 해서 6이 된다.
- 그리고 상황에 따라 extrinsic 이나 bias 등을 포함하면 더 길어질수도(6 이상) 있다. 하지만 r2live 코드를 보면 6으로 설정되어 있는데, 그 이유는 아마도, residual 에서 어짜피 extrinsic 이나 bias 등을 고려하지 않는 경우 (상수처리하거나 아예 term이 없는 경우), 그런 state element 에 대한 Jacobian block이 0이되므로 어짜피 그 변수조절에 기여하지 않기 때문이다 (r2live 의 논문 appendix 의 식 S4 아래 H 참고).
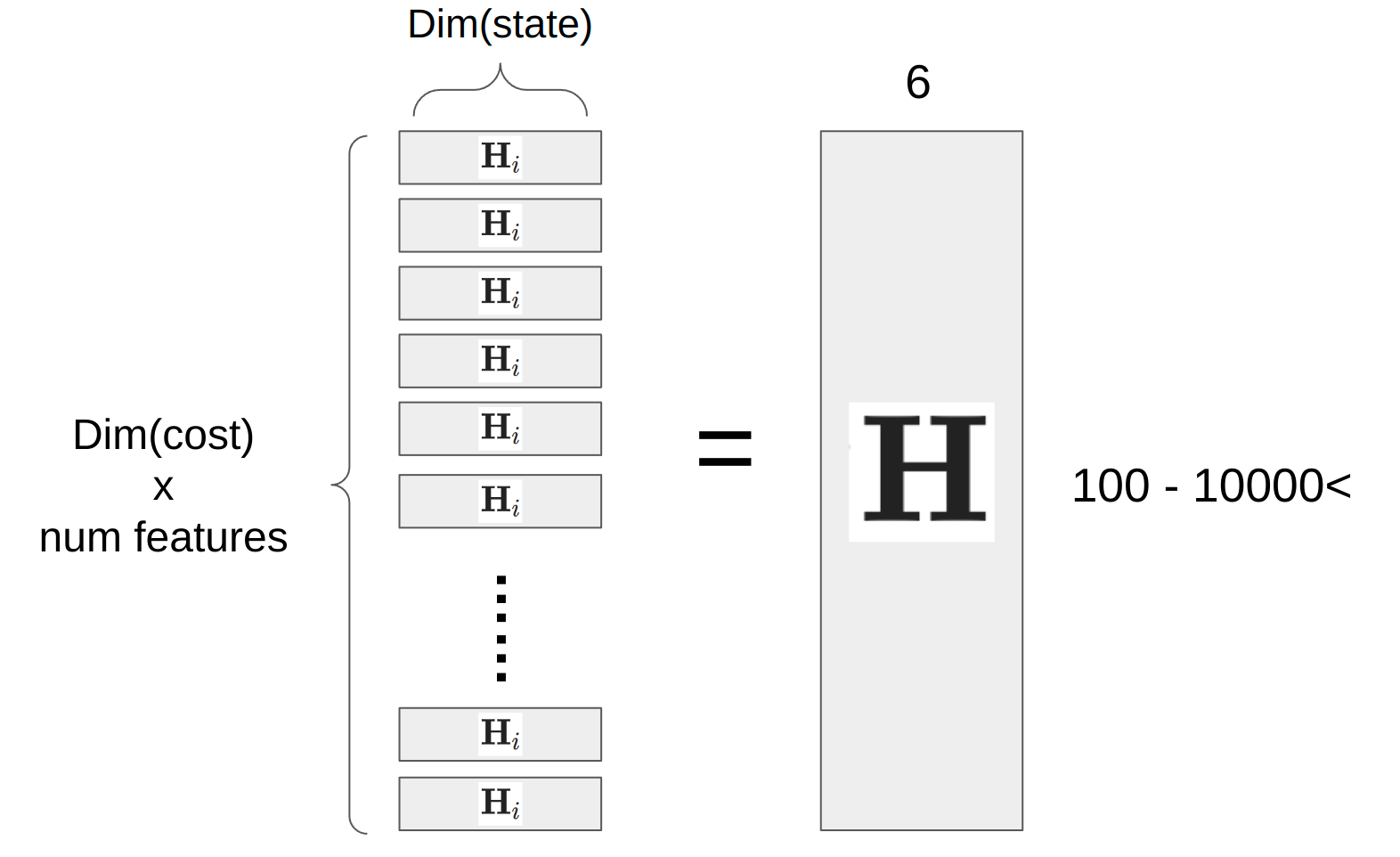
- 그런데 a single image에서 detect 되는 feature point 의 개수나, 혹은 a single lidar scan (e.g., 360 deg horizontal sweep during 0.1 sec) 에는 포인트가 하나만 있는 것이 아니다. 이미지에는 수십-수천개의 피처가 존재할 수 있으며 (이미지 사이즈마다 다르다), lidar 역시 통상적으로 수천개의 (downsampled) 피처 포인트 를 가진다. 이런 포인트 하나 하나마다 위의 residual block (i.e,. $\textbf{H}_i$ for $i=1,2,3,…,$ 수십-수천) 이 존재하게 된다.
- 이를 overdetermined system이라고 부른다.
- 따라서 the slow K: $ \textbf{K} = \textbf{P}\textbf{H}^{\textbf{T}}(\textbf{H}\textbf{P}\textbf{H}^{T} + \textbf{R})^{-1}$ 의 식 안에 존재하는 $\textbf{H}$의 모양은 아마 이렇게 생겼을 것이다.
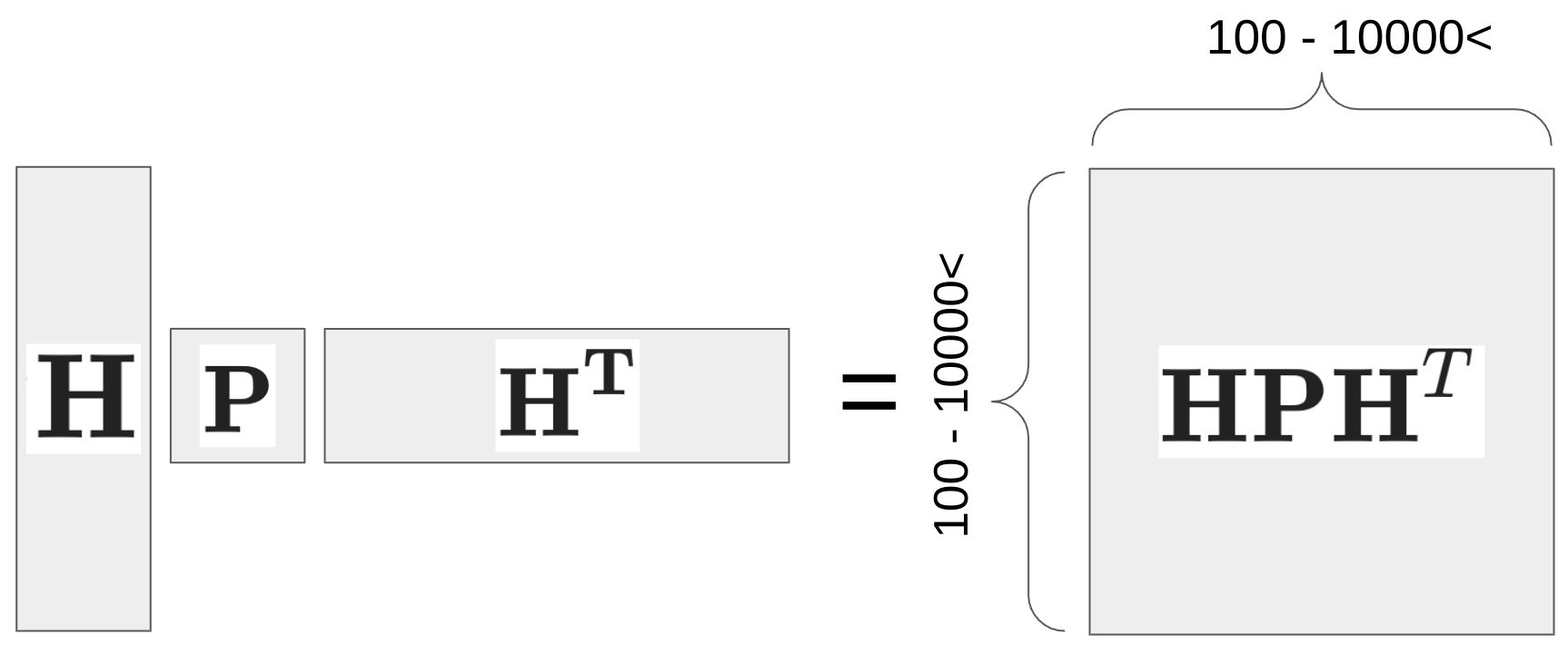
- 이제 거의 다 왔다. The slow $\textbf{K}$ 를 계산하기 위해 우리는 $(\textbf{H}\textbf{P}\textbf{H}^{T} + \textbf{R})^{-1}$ 가 필요하다.
- 그런데 이 matrix inversion 의 비용은 얼마일까? wikipedia 에 따르면, $O(n^{2})$ 보다도 비싼 것을 알 수 있다.
- 즉, 우리는 slow kalman gain 을 계산하기 위해서 $\textbf{H}\textbf{P}\textbf{H}^{T}$ 의 shape 에 제곱배 이상에 비례하는 계산 비용을 치러야 한다. 그런데 그 shape 은 적으면 (image feature의 경우) 수백, 많으면 (liar feature의 경우) 수천 수만 까지도 커질 수 있다.
- 그런데 이에 비해, FAST-LIO에서 제안한 fast kalman gain 에서 inversion해야 하는 대상의 생김새는 이러하다.
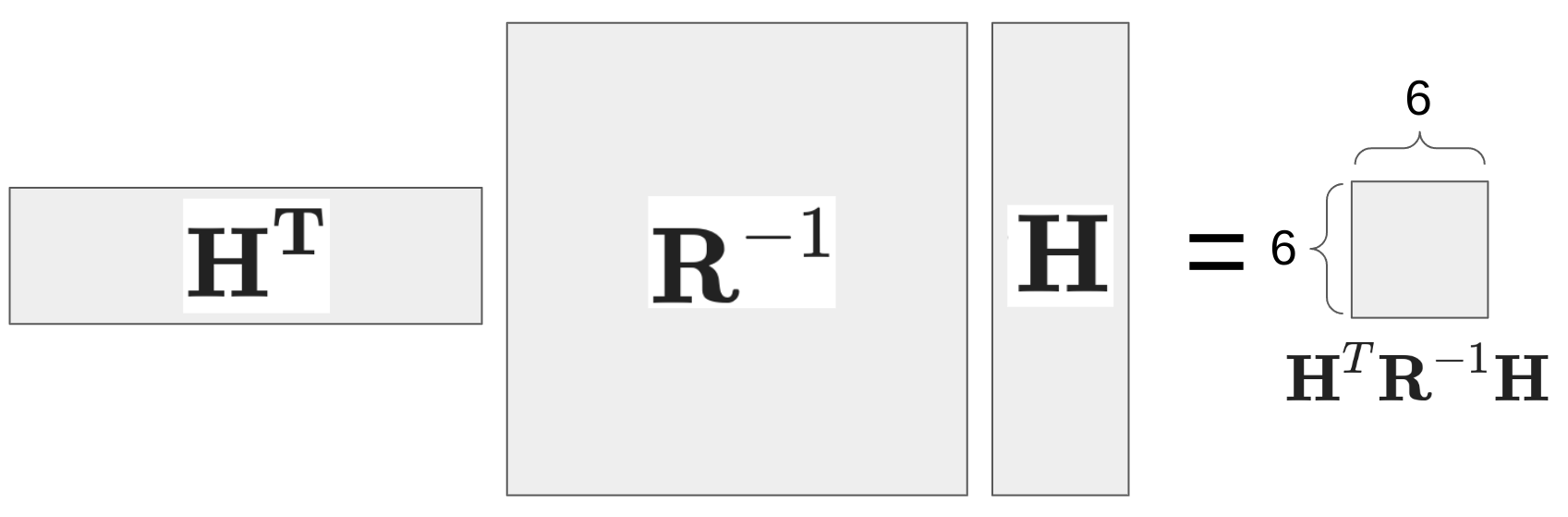
- 훨씬 작음을 알 수 있다!
- slow K 에서 inverse를 수행해야 할 matrix 크기가 작게 잡아서 60x60이라고 가정하면 (i.e., $n=60$), fast K 에서 inverse 를 수행해야 할 square matrix 의 $n=6$ 대비 10배가 크다. wiki 에 따르면 matrix inversion 의 time complexity 는 $O(n^{2.373})$ 정도이지만 어림잡아 $O(n^{2})$ 라고 하면, 100배의 시간이 더 소요될 것으로 예측해볼 수 있다.
- 과연 진짜 이만큼 느려지게 될 지 직접 실험을 통해서 알아보자.
실험
- 실험 세팅
- 실험을 위해 r2live 코드를 이용하였다. 그리고 r2live github readme 에서 공개되어 있는 저자의 HKU 데이터를 사용하였다. CPU는 11th Gen Intel(R) Core(TM) i5-11400F @ 2.60GHz 을 이용하였고, 특별히 core 제한은 하지 않았다.
- Time cost 측정을 위해 Faster-lio repository에 있는 timer class 를 가져왔다.
- 그리고 conventional 한 Kalman Gain 이 구현되어 있지 않기 때문에 직접 구현해준다. 크게 어렵지 않다.
- r2live 는 lidar 와 visual 기반에 각각 Kalman Gain 계산하는 부분이 있다. 그 중 편의상 visual part 에 대해서만 테스트를 진행해보았다 (Kalman Filter 자체는 abstract 한 engine 이기 때문에 개념(Fast-lio가 fast kalman gain을 제안한 기여)은 동일하다).
- See this line of codes. 실험코드는 다음과 같다.
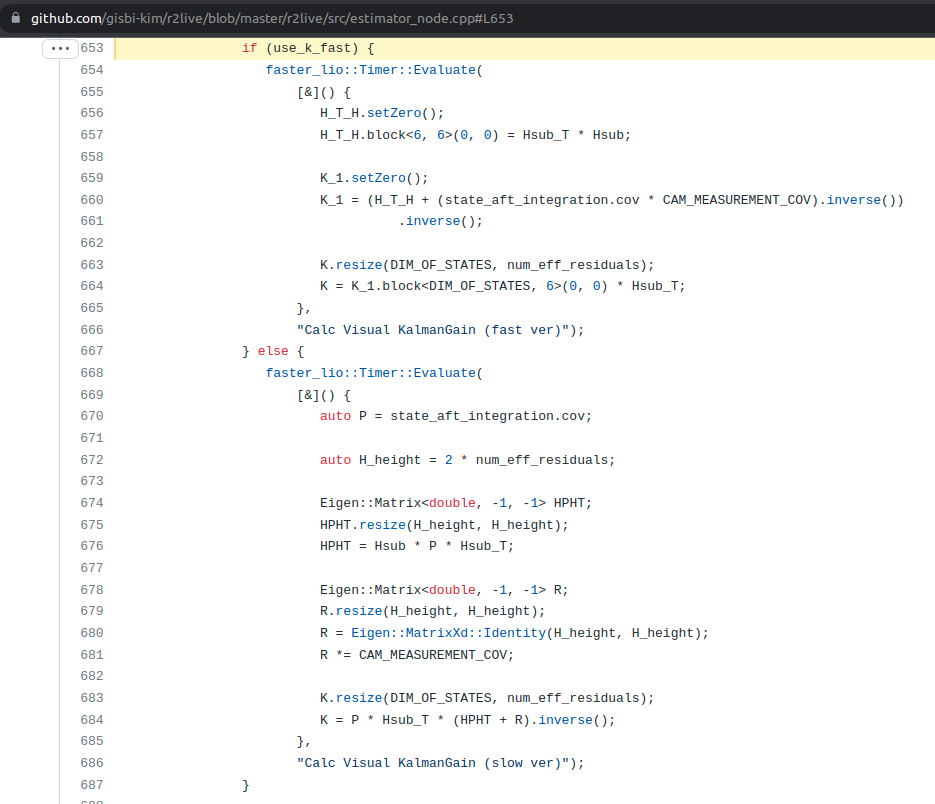
- See this line of codes. 실험코드는 다음과 같다.
- 실험 결과
- 실험 수행 과정 및 결과는 아래 비디오에 자세하게 나와있다.
- ps. 이 실험을 reproduce 해보려면:
- docker/run 에 있는 repository의 volume 경로를 본인의 것으로 수정하길 바란다. 그리고 demo.launch 파일에서 fast version 의 kalman gain을 사용할지 말지 boolean param 으로 조절할 수 있도록 하였다. docker 를 이용해서 r2live 를 실행하는 과정에 대해서는 다른 비디오 <Running R2Live using Docker> 에서 자세하게 소개하였으니 참고.
- ps. 이 실험을 reproduce 해보려면:
- 실험 결과를 정리해보면,
- 위 데이터셋에 대해, a single image 에서 50-100 개 정도의 feature correspondences 가 나온다.
- fast or slow 어떤 버전의 kalman gain을 사용하든 accuracy 측면에서는 거의 동일하게 동작하는 것처럼 보인다 (TODO: 실제로 같은지 K값 찍어보기)
- fast version 의 kalman gain을 계산하는 시간은 0.026ms 정도가 소요된다.
- slow version 의 kalman gain을 계산하는 시간은 2.6ms 정도가 소요되었다. 약 100배의 시간이 소요된 셈.
- 이는 앞서 matrix inversion의 time complexity에 근거해서 유추했던 것과 유사한 magnitude of order 이다.
- 실험 수행 과정 및 결과는 아래 비디오에 자세하게 나와있다.
- Lessons
- image feature 에 대해서, state_dim=6 이고, num_features=50-100 이면 약 10배의 size 로 근사할 수 있었고, 실제로 이의 제곱배 이상의 time cost 가 발생함을 확인하였다.
- 그리고 lidar feature 는 보통 1000-10000개 까지도 발생한다. 현대의 3D 라이다가 주는 하나의 스캔이 수만개의 포인트를 가지고, 이를 적절히 downsampling 해서 사용한다고 하더라도 수천개의 포인트가 존재한다. 6000개(까지도 필요없을 수도 있지만 계산의 편의상)라고 가정하면 state_dim=6 에 비해 1000배의 size 를 가지는 matrix 를 inversion 해야되게 된다. 그러면 이론적으로는 최소 1000 * 1000 배의 시간이 걸릴 것이라고 예측해볼 수 있겠다. 그러면 (위와 동일한 HW기준) 0.026 * 1000 * 1000 = 26000ms = 26 sec 으로써 이제는 real-time 이 불가능하게 된다. lidar scan이 보통 10hz라고 가정하면 (실제로는 front-end를 포함해서) 0.1s 내에 update가 되어야 real-time이라고 할 수 있다.
- TODO: 과연 그러한지 lidar 의 kalman gain에 대해서도 직접 측정 해보자.
- 그리고 또 하나 문제가 될 수 있는 것은, slow version K에서 inversion 하는 matrix 의 크기는 feature correspondences의 개수에 의존적이기 때문에, time cost 가 scene 마다 달라질 수 있다. 이는 특정 환경에서 발생한 적은 time cost만을 측정하여 자원의 upper bound 를 할당해두는 경우, 환경이 달라질 경우 문제가 될 수도 있다. 반면 fast version K는 항상 6x6 의 inversion을 수행하기 때문에, 소요되는 시간 역시 매 image 마다 유사함을 알 수 있다 (see the Timer::DumpIntoFile, 평균이 아닌 모든 frames 에 대한 time cost 가 기록되어 있다).
PS. 재미난 사실들
- 속도 개선: 극한의 깎기
- r2live 코드를 보면
K_1 = (H_T_H + (state_aft_integration.cov * CAM_MEASUREMENT_COV).inverse()).inverse(); K = K_1.block<DIM_OF_STATES, 6>(0, 0) * Hsub_T;- 이 Kalman Gain 구현이 FAST-LIO의 식20 에서 언급한 것과는 약간 다른 것을 볼 수 있다.
- 즉 size 가 큰 $\textbf{R}$ matrix 를 생성조차 하지않고 scalar 값을 곱하는 것으로 대체하였다. 이는 each measurements in a single image (or a single lidar scan) 이 동일한 weight 를 가진다고 가정할 경우, $\textbf{R} = r\textbf{I}$ 와 같이 scaled identity 로 가정할 수 있다. 이 식을 원래 식 $ \textbf{K} = (\textbf{H}^{T}\textbf{R}^{-1}\textbf{H}+\textbf{P}^{-1})^{-1}\textbf{H}^{T}\textbf{R}^{-1}$ 에 대입하면 위의 코드와 같이 $\textbf{R}$ matrix 가 사라진 형태를 얻을 수 있다.
- r2live 코드를 보면
- 성능 개선: GICP 따라하기
- FAST-LIO의 후속작은 FAST-LIO2 라기보다는(FAST-LIO2는 그냥 저널버전 느낌..), VoxelMap 이라고 생각한다.
- FAST-LIO에서는 단순한 point-to-plane loss (distance에 normal이 곱해짐) 을 사용하였다면, VoxelMap은 GICP-like Loss 를 사용하였다. 즉, per point 마다 다른 covariance 를 적용하였다. 재밌는 것은 구현이다. VoxelMap의 코드를 보면 r2live 의 fast-lio부분과 거의 동일한 코드베이스를 사용하고 있음을 알 수 있다. 대신 fast-lio (r2live) 와 달리 $\textbf{H}^{T}\textbf{R}^{-1}$을 명시적으로 계산해준다. 이 역시도 $\textbf{R}$을 별도로 만들어서 곱하는게 아니라
MatrixXd Hsub_T_R_inv(6, effct_feat_num);와 같이 $\textbf{H}^{T}\textbf{R}^{-1}$ 라는 matrix 를 아예 처음부터 생성해서 다루고 있는 것도 재밌는 부분이다. 어쨌거나 VoxelMap에 와서는 per-point 마다 다른 weight 를 부여할 수 있게 되었고, 그 결과 아래 코드를 보면 FAST-LIO의 식20 에서 언급한 fast kalman gain $ \textbf{K} = (\textbf{H}^{T}\textbf{R}^{-1}\textbf{H}+\textbf{P}^{-1})^{-1}\textbf{H}^{T}\textbf{R}^{-1}$ 과 이제 완벽히 format이 동일해진 것을 알 수 있다.

결론
- FAST-LIO는 Kalman Gain의 형태를 조작함으로써 problem solving 시간 개선을 이루었다.
- 기존의 잘 알려진 K가 항상 slow 한 것은 아니다. 하지만 low-level features의 geometric optimization 을 수행하는 SLAM 문제에서는, constraints 의 개수가 매우 많은 overdetermined system 이 일반적이며, 이 경우 K 계산이 slow 해지게 된다.
- 그 현상을 좀 더 이해하기 쉽게 그림(matrix-illustrated)으로 그려보았다.
- 그리고 실제로 그러한지 적용 전/후 실험을 수행해보았다.
