Error-state Kalman Filter 란?

• 최근 SLAM 학/업계에서는 visual은 OpenVINS, lidar는 Fast-LIO 가 대세가 된 듯하다.
  • 이 둘은 모두 on-manifold EKF 혹은 error-state Kalman filter 라고 불리는 방식을 사용하고 있다.
• 그래서 Error-state Kalman Filter (ESKF) 에 대해 공부해보았다.
• 최대한 쉽게 큰그림 위주로 이해해보자.

큰 그림

• 일단 ESKF에 대해 이야기 하려면
  1. EKF (Extended Kalman Filter)를 알아야 하고
  2. 그 전에 KF (Kalman Filter)를 알아야 한다.
  3. 그리고 GN (Gauss-Newton) Opt 에 대해서도 이해해야 한다.
• 뭔가 많아 보이지만, 큰 그림에서 수학없이 이야기해보는 것이 이 포스트의 목적이다.

KF 톺아보기

• KF 에 대한 (수학적) 설명을 여기서 늘어놓을 생각은 없다..
  • KF를 약간 무식하게 한줄 요약하자면 1. 저질러보고, 2. 수정하기, 라고 할 수 있다.
    • 예를 들어 현재 벽으로부터 내가 1m 떨어져서 서있음을 안다. 그리고 내 보폭 한 칸은 50cm 정도 되고 내 팔길이는 50cm 라고 하자. 내가 앞으로 한칸 움직이면 나는 벽으로부터 얼마나 떨어져있을까?
      1. 저질러보기: 일단 움직이자! 50cm 라고 치자. 그러면 나는 벽으로부터 100-50 = 50 cm 만큼 떨어져있겠지?
         • 하지만 문제는 보폭이 항상 정밀하게 딱 50cm 일리는 만무하다.
      2. 수정하기: 그래서 팔을 한번 뻗어보았다. 근데 팔을 끝까지 쭉 뻗었는데도 공간이 조금 남네. 그러면 50cm 보다는 일단 덜 간 건 알겠다. 그럼 아까 50cm 떨어져있다고 저질렀던 예측값을 조금 수정해주면 되겠다.
    • 근데 팔길이로 길이를 대충 재는 것도 엄청 정밀하지는 않은데.
      • 나는 벽으로부터 60cm 떨어져있다고 해야 하나..? 55cm 떨어져있다고 해야 하나..? 보폭과 팔길이기반측정 의 결과를 서로 다른 신뢰도에 기반해서 어떻게 적절히 잘 융합할 수 없을까? 그것에 대한 수학적인 기계적 과정을 제공하는 것이 KF라고 할 수 있다.
  • 이에 대한 공부자료는 An Introduction to the Kalman Filter (2006 ver) 를 추천한다.
    • KF 공부자료야 워낙 많지만… 이게 가장 분량도 적절한 듯하다 (너무 생략되어있거나 너무 쓸데없이 입문자에게 불필요하게 많지않다).
    • 95년에 처음 나온 report 인데 현재 (2022.09) 무려 10000회 인용이 넘었다. 이 report 는 되게 간결한 편이며 더욱 자세한 유도 등은 여기에 reference 들이 잘 추천되어 있으므로 (e.g., Maybeck79) 추가적으로 더 공부하고 싶으면 참고하면 좋다.
• 요약하자면 KF는 prior (저질러 본 것)와 measurement (재 본 것) 사이의 weighted sum (두 결과 토대로 수정한 것)을 해주는 장치이다.
  • 이 때 고정된 상수로 융합하는 게 아니라, a posteriori 의 covariance 를 minimize 하는 것을 cost 로 하여 최적 gain 을 결정하는 방법이다 (따라서 Kalman gain 은 blending factor라고도 불린다).
  • 암튼 핵심은 KF는 방금 설명했듯 a posteriori 의 covariance 를 minimize 하는 것을 목표로 하기 때문에, optimal estimator 라고 불린다.
    • 혹은 위키를 보면, KF는 linear quadratic estimation (LQE) 라고도 불린다고 나와있다.
      • covariance 는 그 정의상 random variable error vector의 제곱꼴이기 때문이다.
• 잡썰
  • ps1. Phil’s Lab 의 유튜브 영상도 KF에 대해 정말 이해하기 쉽게 잘 설명해준다. 추천! (1편, 2편, 3편, 4편)
    • 2편에서 상수 weight 비율로 fusion 하는 (e.g,, 0.5 and 0.5) complementary filter 를 먼저 보여주고 EKF로 넘어가는 스토리가 아주 일품이다. 그리고 실제로 IMU 센서 데이터를 통해 결과를 보여주기 때문에 KF 가 현실세계와 동떨어진 무언가로 느껴지지 않는다.
  • ps2. KF에서 prior 라는 용어가 꼭 매우 최초의 어떤 정보만을 의미하지는 않는다. KF는 Bayesian filtering 이며 Bayesian filtering 의 철학은 현재의 최적값이, 다음 턴의 사전정보가 된다, 이기 때문이다. 즉 현재의 posterior 가 다음 턴의 prior 로써 역할하는 것.
    • 그나저나 Bayesian filtering 이야기가 나온 김에… KF는 원래 상당히 최적화 스러운 (== least square optimization 스러운) 느낌으로부터 유도 되었지만 (방금 말했듯 cov를 최소화 하도록), 그 nature 를 들여다보면 Probabilistic한 면이 있다. 이 이야기가 The Probabilistic Origins of the Filter 라면서 위에서 추천한 자료에도 나온다. 또는 Särkkä, Simo. Bayesian filtering and smoothing. No. 3. Cambridge University Press, 2013. 이 책의 앞부분을 참고 (요약 1편, 요약 2편).

EKF 톺아보기

• 이제 우리는 KF에 대해 알았다. 그럼 EKF로 넘어가보자.
  • (E-, ES-) KF류를 구성하기 위해서는 가장 먼저 system model이 정의되어야 한다.
    • 1. process model 과 2. measurement model 이 있다.
  • 앞서 공부자료 An Introduction to the Kalman Filter (2006 ver) 의 식 1.1, 1.2 에서처럼 이 모델들이, 우리가 알고싶은 state 나 measurement vector 와 그저 matrix 곱으로 이루어져 있으면 linear 하다라고 한다.
  • 그런데 현실세계에서는 다양한 이유들로 인해 nonlinearity가 생긴다.
    • state 가 nonlinear 할 수 있다 (e.g., rotation 을 추정하고 싶은 경우)
    • 혹은 measurement model 이 nonlinear 할 수 있다 (e.g., 제곱, exponential 등등이 들어가는 복잡한 형태)
  • 그래서 이런 nonlinear 한 process model $f(\cdot)$ or observation model $h(\cdot)$ 을 테일러 급수로 편 다음에 1차 근사 (== linear term만 남김) 해서 쓰겠다는게 EKF이다.

ESKF 톺아보기 … 전에

• 그럼 EKF와 ESKF는 무엇이 다른가?
• 이 이야기를 하기 전에 우리는 잠시 KF 라는 것 자체로부터 멀어질 필요가 있다.
• 즉 ESKF 와 EKF는 이렇게 달라, 하고 그 물질적인 면을 보고 외우는 것보다, 무엇보다 ESKF가 왜 필요하게 되었는지를 살펴보자는 것이다.
  • 키워드 힌트: EKF on manifold
    • 즉, manifold 에서 EKF를 하려면 뭔가 좀 특별하게 care 해줘야 할 게 있다는 것인데. 이게 뭔소린가 하니 차차 알아보자.
• 앞서 KF도 optimal estimator 라고 했다. 즉 covariance 라는 squared loss 를 최소화 하는 최적화기기 인 것이다.
  • 즉 이부분에서 KF는 least square optimization 의 대표주자인 Gauss-Netwon optimization (GN) 을 닮았다.
    • GN (or can be LM, just damping 이 추가된 GN)이 변화량이 어느정도보다 작아질 때까지 계속 iteration 을 반복해서 $\delta \textbf{x}^*$ 를 찾아가는 것이라면 (for details, see the post: Nonlinear ICP 밑바닥부터 구현해보기),
    • KF는 최적의 weight 비율을 한방에 딱 찾아내서 딱 한번만 update 해주는 GN optimizer 라고 생각해볼 수 있다는 것이다.
      • ps1. 완전히 같다는 게 아니라, 그 느낌만 공유하자… GN에서는 명시적인 prediction step이 없으므로 (그저 initial value가 주어짐) GN은 여러 measurement (squared) loss의 weighted sum을 minimize 하는 updator 부분만 있다고 생각해볼 수 있겠다.
      • ps2. 물론 KF에서도, 한번의 propagate 에 대해 여러번의 (수렴할 때까지) update 를 해주는 방식으로 iterative 하게 구성할 수 있긴하다 (예시: se3_localization_iekf)
  • 그래서 GN 이야기를 좀 더 해보자.

GN 톺아보기

• GN에서 개념 자체는 너무 간단하다.
  • 기본적인 개념에 대해서는 늘 추천하는 Grisetti 교수님의 ICRA tutorial 자료를 보고 오기를 추천… 하고 여기서는 GN 에 대해서는 설명하지 않기로 하고.
  • 결과만 이야기하자면 GN이란 그저 $J^{T}J \delta \textbf{x} = -J^{T}e$ 를 푸는게 전부이다.
    • 이걸 풀어서 나온 $\delta \textbf{x}^{*}$ 를 기존 해 $\textbf{x}$ 에 더해주면 된다. 그리고 $\delta \textbf{x}$ 가 충분히 작다면 수렴한 것으로 보고 iteration 을 종료하면 된다. 이걸 from scratch (밑바닥부터)로 구현해본 것이 the previous post: Robust Optimization Tutorial.
  • 그런데 이부분은 정말 기계적인 부분이고. 중요한 지점은 저 $J$ 란게 뭐냐, 하는 것이다.
    • ps. (GN에서 명시적인 prediction 은 없으므로) 일단 measurement model 에 대해서만 J가 무엇인지 이야기해보자.
• 제일 큰 그림으로 말해서, $J$는 기울기 이다.
  • 이건 고등학교 미분에서도 나오는 내용. 어쩌구 저쩌구, 미분해서 0이 되는 $x$가 최적값 .. 이런 이야기는 익숙할 것이다.
  • 이 때 그 미분 값이 곧 $J$ 에 해당한다.
  • 그리세티 교수님의 슬라이드 에서 이 얘기를 발췌해오면 다음과 같다.

    

  • 여기서 알 수 있는 건 $J$가 기울기는 기울기 인데, 좀 더 자세히 설명하자면 error (loss)에 대한 $\textbf{x}$ 의 기울기 라는 것이다. 이 때 조심해야하는 것은, 그냥 기울기라고 말하는 것은 too vague 하다는 점.
    • 즉, $\textbf{x}$ 가 변할 때 cost 가 얼마나 변화 하느냐 에 관한 것이다.
      • ps. $J$는 $k$ by $n$ matrix 가 되는데, $k$는 cost vector 의 dimension, $n$은 예측하고자 하는 state vector의 dimension이다.
        • 역시, 앞선 포스트에서 실습을 통해서 이 shape 을 직접 느끼는 것을 추천함: Robust Optimization Tutorial
• 그런데 Grisetti 교수님의 ICRA tutorial 자료 에서 최종적으로 하는 말은 결국 이것이다.
  • state 에 nonlinear 한 element 가 있다면, 그것의 tangent space 에서 update 해주어야 한다.
  • 이게 뭔 말인고 하니, 예를 들어 보면
    • 3차원 공간에서 rotation 은 보통 SO(3) 로 표현되며 이는 3 by 3 matrix 이다. rotation을 최적화 하기 위해서 이를 9-dimension vector 로 만들고, 이 9개의 값을 조금조금씩 조절해서 cost 조절해나가면 될까? 즉 $J$가 $k$ by $9$ 가 되도록 (state 에는 rotation 만 있다고 치자) $J$를 계산해나가면 될까?
    • 그러면 안된다는 것이다.
    • 이런 nonlinear entity (e.g,. rotation) 들은 vector space 가 아니므로, 기존의 기계적인 GN pipeline 에 바로 적용할 수 없다는 것이다.
  • 그래서 해결법은,
    • nonlinear entity 의 접평면 공간 (tangent space)는 국소적으로 vector space라고 할 수 있으므로
      1. 그 접평면 공간에 사는(live) variable 에 대한 error 의 기울기를 계산해주자는 것이다!
         • 예를 들어 rotation 은 국소적으로 angle-axis 라는 3-dim vector 로 표현할 수 있다.
      2. 그러면 cost 를 최소화하려면 접평면 에서 변수를 얼마나 조절해야하는지 알 수 있다.
         • ps. 이 접평면에 사는 변수를 일컬어 Ceres 에서는 local parametrization 라고 부른다 (2.2.0부터는 이름이 manifold로 바뀌었다).
      3. 그런 다음, 접평면 공간에 사는 변수와 원래 공간(nonlinear)에 사는 변수 사이에는 잘 알려진 관계가 있기 때문에, 원래 공간에서 얼마나 해를 조절해야 하는지 알 수 있다는 것이다.
         • ps. 이렇게 원래의 공간으로 최적조절분량을 돌려보내는 것을 retraction 이라고 한다.
    • 관련 실습
      • 이미 앞선 포스트 Robust Optimization Tutorial 에서 SymForce를 이용해서 위의 1-3 step 을 거쳐 rotation 을 최적화 해본 바 있다. 아래 코드처럼 rotation 을 3-dim vector로 parametrization 했었었다. (ps. SymForce 의 장점은, 접평면에서 그래서 기울기를 어떻게 계산해? 와 같은 수학적인 부분을 기계적으로 자동화+최적화 하여 엔지니어가 신경쓰지 않아도 되게 한 것)

        rotvec   = sf.V3.symbolic("Theta") # i.e., angle-axis parametrization
        rotmat   = LieGroupOps.from_tangent(sf.Rot3, rotvec) # for debug, display(rotmat.to_rotation_matrix())
        

    • 관련 논문
      1. 방금 한 1-3 step에 관한 이야기에 대한 정말 자세한 이야기는 A micro Lie theory for state estimation in robotics 에서 소개되고 있다.
         • 이 리포트를 바로 보면 온갖 수학기호가 괜히 어렵게 느껴질 수 있지만, 핵심은 위의 1-3이 전부라 생각한다.
      2. Kalman Filters on Differentiable Manifolds 에도 관련 설명이 잘 나와있다. 아래 그림이 위의 step 1-3 을 시각화 한 것.

         

• 아무튼 이러한 이유로 인해, Grisetti 교수님의 ICRA tutorial 자료 에서는 최종적으로 non-manifold 버전의 GN과 manifold 버전의 GN 두개를 비교하는 것을 보여준다.
  • 여기서 우리가 봐야할 부분은, 그래서 그 두 개가 뭐는 같고 뭐가 다르냐? 하는 점이다.
    • 미리 스포를 하자면, 그게 곧 EKF와 ESKF가 뭐가 같고 뭐가 다르냐? 하는 질문과 일맥상통한다.
  • 비교

    

    • 결론부터 말하자면 두 부분 빼고 전체 기계적인 파이프라인 자체는 완전히 동일하다.
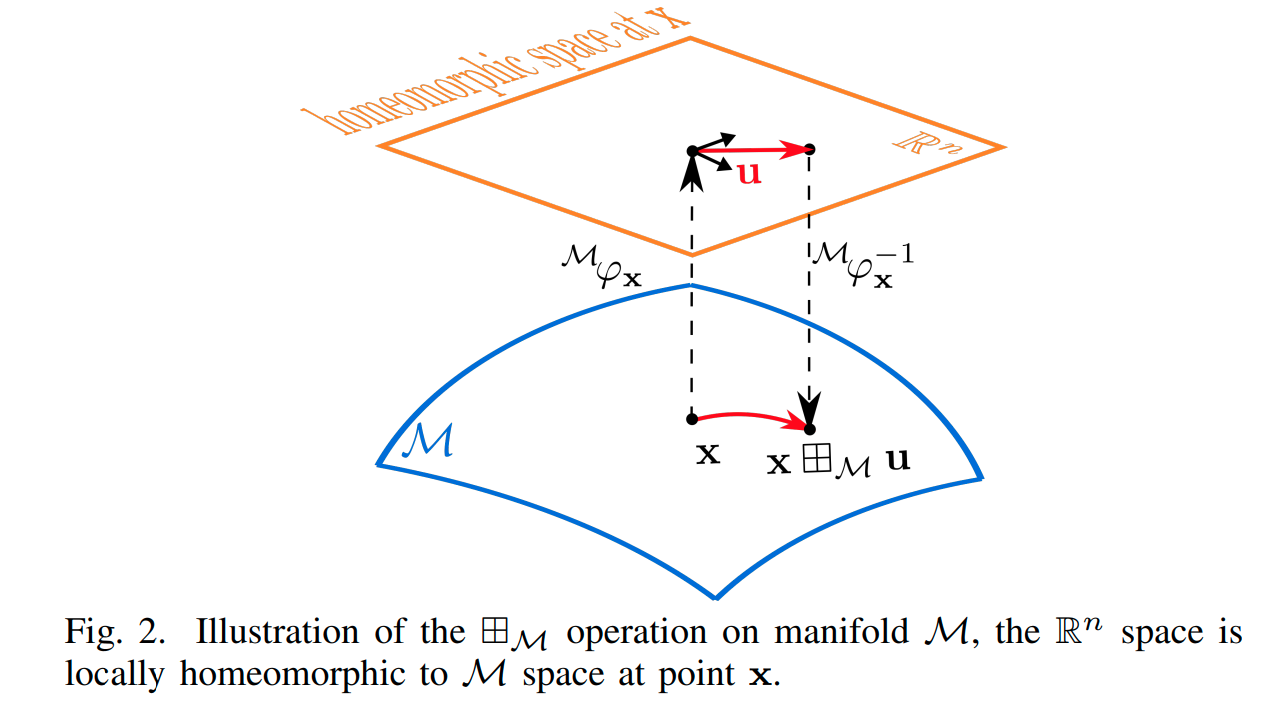
      • 다른 부분 1: 빨강 부분. non-manifold 버전에서는 x와 dx 가 동일한 공간 (e.g., $R^n$)에 살고 있으므로 그저 더하고 빼면 되었다면, manifold 버전에서는 x와 dx 가 서로 다른 공간 (homeomorphic 하다고 한다) 에 살고 있으므로 바로 더해줄 수 없고, 약간의 변환을 거쳐 더해주어야 한다. 이를 편의상 boxminus 와 boxplus 로 표시하고 있는 것. 실제 연산을 위해서는 $\text{Exp}(\cdot)$, $\text{Log}(\cdot)$ 이런 이야기가 나오게 되는데 … 자세한 설명은 여기서는 생략하고 A micro Lie theory for state estimation in robotics 를 보기를 추천함.
      • 다른 부분 2: 파랑 부분. Jacobain 계산이 달라져야 한다. 앞서 Jacobian은 error에 대한 조절하고싶은 변수의 기울기, 라고 이야기했었다.
        • 즉, error 의 조절량이, 어떤 변수에 대한 것인가? 가 명시되어야 한다.
        • manifold(원래 공간) 에서의 variable 에 대한것인가? or tangent space 에서의 variable 에 대한것인가? 의 차이가 위 그림에서 파랑 부분이다.
        • 예를 들어, 위 예시에서 Jacobian은 아래와 같이 달라지게 된다.

          

          • 이는 위 튜토리얼에서 소개하는 ICP라는 application에 한정된 하나의 예시이고…
            • A micro Lie theory for state estimation in robotics 에서 함께 공개한 manif 라는 library는 robotics 에서 흔한 기본적인 연산들에 대해 이런 Jacobian들을 엮어나갈 수 있는 머시너리를 제공한다.

ESKF 톺아보기

• ESKF 가 필요하게 된 이유에 대해서 이제 말할 수 있겠다.
  • Intro에서 OpenVINS나 FAST_LIO같은 state estaimation application 에 대해 이야기했으므로, 여기에 한정해서 생각해보자.
• robot state estimation 을 하다보면 rotation이 항상 문제이다. rotation은 nonlinear 하다.
• 그래서 rotation이 들어간 최적화를 위해서는 통상적으로 이런 과정을 거친다.
  1. 좋은 initial 을 공급한다.
  2. rotation을 tangent space parametrization 으로 표현하여, 그 공간에서 최적화를 수행한 후, retract(==원래 공간으로 보낸다) 한다.
• ESKF도 같은 맥락인 것이다.
  • EKF를 하고 싶은데, 우리가 예측하고 싶은 staet vector에 rotation이 들어있다.
  • 그래서 rotation을 minimal (i.e,. 3-dim) 로 reparametrization 하고, 이 공간에서 KF update 를 수행하자는 것.
  • 즉 error-state 란 앞서 GN예제에서 소개한 tangent space에서 살고 있는 변수, 로 이해하면 쉬울 것이다.
• 근데 그래서 EKF에서 어떤 부분을 다르게 해주어야 하냐? 방금 위에서 비교해온 것과 완전 동일하다.
  1. J 를 error state 전용으로 계산해준다.
  2. 기존 EKF pipeline 에 그대로 태운다.
  3. $\delta \textbf{x}^*$ 를 원래 공간의 initial 해에 boxplus (oplus로도 씀. 실제로는 $\text{Exp}$ 연산.) 를 통해 더해준다.
• 이 얘기가 A micro Lie theory for state estimation in robotics 논문에는 이렇게 설명되어 있다.

  

  • 앞서 이해를 돕기 위해 먼저 소개한 GN 예제에서는 prediction 부분은 없으므로, correction 부분을 위주로 비교해보면 이해하기 좋을 것이다.
    • 일부러 앞의 GN 예제에서 사용하였던 부분과 같은 강조색깔을 사용하였다.
  • 이 논문에서도 EKF와 ESKF가 (correction step에서) 다른 점은 딱 두가지라고 이야기하고 있다. (위 그림에서 빨강 밑줄 친 부분)
    1. manifold 와 tangent space 사이의 연산을 할 수 있는 oplus 사용
    2. Jacobian을 tangent space에서 계산
       • ps. correction (update) step에서 사용하는 measurement model을 보통 $h(\cdot)$ 으로 많이 쓰기 때문에, $ error = h(\cdot) - z $ 의 미분을 $H$ 로 표기하였다 (z는 상수이므로 날아가고). 즉 여기서 H 는 Hessian ($= J^T J$) 이 아니라, 앞서 이야기해왔던 $J$ 이다! 헷갈리지 않도록 문맥을 잘 살피자.
       • $H$ (i.e,. $J$) 가 Lie theory 를 통해 계산되고, 이것이 결과적으로 $K$에 영향을 주게 된다. 즉, tangent space에서의 blending factor 를 잘 계산해주는 것이다.
  • 위의 예시가 코드로도 있다: manif/examples/se2_localization.py
    • 실제로 Jacobian부분은 manif 가 알아서 해주고 있기 때문에, retract 하는 부분 (i.e,. + SE2Tangent(dx)) 을 제외하면 코드 상에서 겉보기로는 EKF와 크게 다를 바가 없게 느껴진다.
  • Note:
    • 물론 GN과 달리 (ES)KF에는 prediction step 이 있기 때문에, 이 때 tangent space 에 살고 있는 변수(==error state)의 covariance를 propagation 하는 과정이 추가적으로 필요하다. 그것이 위의 그림에서 왼쪽 부분에 해당하는 것이고, 여기서 $P$는 error-state 의 covariance 임을 주의하자.
      • 결국 이를 수행하기 위해서는 error-state 에 대한 (discrete-time) kinematics 를 유도하긴 해야 한다. (즉, process model을 error state version으로 만들어야 함)
      • 이 부분에 대해서는 Quaternion kinematics for the error-state Kalman filter 에 아래와 같이 잘 설명되어 있음. 자세한 설명은 해당 문서를 보시길 …

        

        • 이 $\textbf{F}$ 를 이용해서 covariance propagation 이 이루어진다.
          • 예를 들어, 코드에서는 (이 예시에서는 imu kinematics는 아니긴 하지만) P = J_x @ P @ J_x.transpose() + J_u @ U @ J_u.transpose() 이렇게.
        • ps. FAST_LIO 논문에서도 그래서 저런 matrix (식 (7))를 적어놓은 것을 볼 수 있다. OpenVINS docs 에서도 error state propagation 에 대해 설명하고 있다.
• ps.
  • Error-state space (tangent space) 에서의 Jacobian 계산법에 관련하여, Quaternion kinematics for the error-state Kalman filter 에 좀 더 자세하게 설명이 되어 있다.

    

    • 여기서 $H$는 앞서 계속 말했듯, Jacobian, 기울기, 즉 tangent space에서 변수를 조절하면 error cost 가 얼마나 변할까하는 저도. Chain rule 로 이걸 x 에 관한 미분과 dx 에 관한 미분의 두 term으로 쪼개어 보았다 (식 277).
    • 그런데 식 279를 보면 rotation term 외에는 모두 identity 임을 볼 수 있다. 즉, 예를 들어, 예를 들어 translation 부분은 vector space이기 때문에 원래 공간과 tangent space 가 동일한 것.

결론

• 웹에서 error-state kf 라고 검색했을 때, 자료가 많이 나오지 않아 겸사겸사 정리해보게 되었다.
  • 예를 들어서 토론토대 켈리 교수님께서 짧은 강의로 쉽게 설명해주고 계시지만, 아쉬웠던 부분은 왜 ESKF 를 사용해야 하는지 매우 요약해서 마지막에 잠시 summary로 나오고 끝나버린다…
• 요약
  1. ESKF는 rotation 등 nonlinear 한 state element 들을 효과적으로 최적화 하기 위해 필요하게 되었다.
     • 즉. On-manifold EKF 라고 할 수 있을 것이다. (vector space인) tangent space 에서 최적값을 구한 후 원래 space로 올려준다.
  2. EKF나 ESKF 기계적인 형태는 같다. (예시: manif/examples/se2_localization.py)
  3. 다른 점
     1. prediction step: error state 에 대해 process model 을 세워주어야 한다. 이를 이용해서 error state 의 covariance 를 propagate 해준다.
     2. correction step: Jacobian을 nominal state 에 대해 구하는 것이냐 error state 에 대해 구하는 것이냐 하는 것이 EKF와 ESKF의 차이이다. 결과적으로 Kalman gain $K$ 가 tangent space 에서 weight blending 을 잘 할 수 있도록 만들어진다.
• 추천자료 정리
  1. Quaternion kinematics for the error-state Kalman filter
  2. A micro Lie theory for state estimation in robotics
  3. Kalman Filters on Differentiable Manifolds
     • 위 3개를 순서대로 보는 것이 좋을 듯 하다.
       • 위 세 논문들이 robot state estimation 문제를 중점적으로 다루고 있고, error-state / tangent space / manifold / Lie theory 와 같은 개념들이 한데 나오기 때문에 좋은 듯하다.
       • 보는 순서의 이유는 1,2,3 순으로 설명이 더 친절한 듯 하기 때문.
     • others
       • FAST-LIVO 논문을 보면, an iterative optimization has been proven to be equivalent to an iterated Kalman filter [21]. 이런 말이 있다. 93년도 The Iterated Kalman Filter Update as a Gauss-Newton Method 라는 논문. ESKF와 GN 사이의 관계에 대해 알아볼 수 있겠다.
• ps.
  • 유사하게 GN 관점에서 imu kinematics 를 on-manifold 에서 다루는 시도 중 가장 유명한 방법은 IMU Preintegration on Manifold for Efficient Visual-Inertial Maximum-a-Posteriori Estimation 이다.
    • 이 방법과 같은 batch (sliding window 포함) 최적화 입장에서는 recursive nature 가 없기 때문에, error state 의 covariance propagation 에 대해서는 less care 해도 되었지만, 대신 그러면 매우 빠르게 들어오는 IMU measurement 들을 모두 다 residual 로 넣어줘야 하냐? 비용이 너무 비싸다, 라는 문제가 있었다. 그래서 이 논문은 preintegration 을 통해 이를 해결한 것 (물론 reference보면 preintegration이란 개념은 이미 있었지만 그걸 on-manifold 에서 했다는 것이 이 논문의 포인트).
  • 그래서 암튼 보다보면 On-manifold GN과 ESKF가 상당히 닮아 있음을 알 수 있다.
    • 결국 recursive nature 를 가지는지 여부에 따라 이후 GN vs KF 계열의 맛이 달라지게 된다.
      • 즉, error state process model을 다시 세우는 데 조금 더 노력을 들여야 하는지,
      • 아니면 수많은 imu measurements 들을 하나의 a single measurement 로 압축해서 효율적인 batch GN optimization 을 가져갈지, 와 같은 고민들.