A micro Lie theory 논문이 어렵다면 …
- 이 글을 먼저 읽어보자.
- a.k.a A nano Lie theory!
개요
- 앞의 블로그 튜토리얼 및 예전 블로그 에서도 맨날 정리하는 rotation 이야기를 다시 한번, 좀 더 consice하게, 해보려고 한다.
- 이른바 Nano Lie Theory!
- Joan Sola 의 A micro Lie theory for state estimation in robotics 를 읽기 전에 톺아보고 가면 좋은 이야기들을 수학없이 적어보았다.
- 중요한 것은 How 보다 Why이다. Lie theory를 왜 알아야 하는가?
- micro 보다 좀 더 간결하게 이야기한다는 측면에서 nano Lie theory.
Nano Lie Theory
엔지니어의 일
- 우리는 어떤 변수들의 최적값을 알고싶다.
- 우리가 알고싶은 값들의 모음은 vector (== multi dimensional 1-d tensor) 이다. let it $\textbf{x}$.
- 그리고 그 변수들이 만족해야 하는 어떤 제약들이 주어진다.
- 예를 들어 어떤 뜨거운 물체를 감시하는 로봇이 있다고 하자. 그 로봇은 뜨거운 물체 주변을 어떻게 돌면서 감시해야할까?
- x = (로봇의 위치, 로봇의 자세, 로봇이 느끼는 온도) 라고 하면,
- 자세 제약: 로봇의 자세는 그 물체를 최소한 어느정도 이상으로는 수직에 가깝게 바라보아야 하며,
- 위치 제약: 로봇의 위치는 그 열원을 잘 감시하기 위해 어느정도 거리 까지 가까워지려고 노력해야한다.
- 온도 제약: 하지만 그 때 로봇 자체가 너무 뜨거워지면 기능을 할 수 없으므로 그 물체에 너무 가까워지면 또 안된다.
- 그 제약들을 만족하는 최적값 $\textbf{x}^{*}$ 를 찾고싶다.
최적화의 본질 1: Ax = b
- 이 최적화라는 것은 항상 $\textbf{A}\textbf{x} = \textbf{b}$ 꼴이 된다.
- ps. 왜 그런지 자세한 설명은 생략한다. 이에 대해서는 Numerical Optimization 이라고 검색해서 나오는 여러 텍스트북들을 추천한다. 대표적으로는
Nocedal, Jorge, and Stephen J. Wright, eds. Numerical optimization. New York, NY: Springer New York, 1999.. 현재 인용이 40000회가 넘는다.
- ps. 왜 그런지 자세한 설명은 생략한다. 이에 대해서는 Numerical Optimization 이라고 검색해서 나오는 여러 텍스트북들을 추천한다. 대표적으로는
- 사실 현실 세계에서는 $\textbf{A}\textbf{x} = \textbf{b}$ 와 같이 제약들이 예쁜 매트릭스 곱으로 딱 떨어지지 않고, $\mathcal{A}(\textbf{x}) = \textbf{b}$ 와 같은 어떤 함수 형태로 제약이 존재한다 (… 정말 아무 예를 들자면 $(\textbf{A}\textbf{A}^{T})^{-1}\textbf{x} + \textbf{x}^{T}\textbf{A}\textbf{x} = \textbf{b}$)
- ps. 이를 현실세계는 nonlinear 하다라고 부른다.
- 아무튼간에 무조건 저 형태(더도말고 덜도말고 딱 $\textbf{A}\textbf{x} = \textbf{b}$ 모양새) 를 만들어 내는 것이 관건이다. 그 이후부터 이제 규칙적인 최적화 메커니즘이 돌기 시작할 수 있기 때문이다.
- ‘규칙적인 최적화 메커니즘’ 이란 ‘매우 잘 정립된 기계적인 과정’ 을 의미한다. 즉 아주 계산기스러운. 예를 들어 $1+1$ 을 수행하면 무조건 2가 나올 수 밖에 없는 산수 그 자체.
- $\mathcal{A}(\textbf{x}) = \textbf{b}$ 라는 모양을 $\textbf{A}\textbf{x} = \textbf{b}$ 라는 형태로 만들어내는 것이 테일러 expansion 기법이다 (Power series 로 편다, 와 같이 말하기도 한다).
- 그리고 이 때의 $\textbf{A}$의 모양새에 따라 $\textbf{A}$는 여러 서로 다른 성격을 지닐 수 있게 된다.
- $\textbf{A}$의 성격은 최적화의 결과에 영향을 줄 수 있다. 따라서 저 $\textbf{A}$의 모양새를 이해하는 것이 중요하다.
- 기초적인 것만 얘기하면 under-determinant, over-determination 이런 이야기를 할 수 있겠다. 혹은 저 $\textbf{A}$가 dense 하냐 sparse 하냐 이런 것도 중요한 주제이다. 그래서 최적화를 위해서는 기초적으로 선형대수학이 중요하다고 이야기하는 것이다. 모든 공학적 문제와 모든 최적화는 $\textbf{A}\textbf{x} = \textbf{b}$ 형태의 제너럴한 포맷으로 결국 귀결되기 때문이다.
- 아무튼 $\textbf{A}\textbf{x} = \textbf{b}$ 라는 식을 만족하는 최적값 $\textbf{x}^{*}$ 를 구하는 것이 우리의 목표이다.
최적화의 본질 2: Iterative Optimization on vector space
- $\textbf{A}\textbf{x} = \textbf{b}$ 을 푸는 과정은 대체로 (아니 사실 실제 문제에서 모든 경우…) iterative 하게 이루어진다.
- 예시 키워드: Gauss-Newton
- 이 때 iterative 라 함은 $\textbf{x}$ 의 최적값이 closed form으로 뙇 하고 바로 나오지 않는다는 것을 의미한다.
- 대신에 우리는 $ \delta \textbf{x}$ 의 최적값을 구한다. 그 최적값을 $ \delta \textbf{x}^{*}$라고 하자
- ps. 굳이 첨언하자면 (자세한 notation 설명은 언제나 늘 옳다).. $ \delta \textbf{x}$ 란 당연히 델타 곱하기 $x$ 가 아니다. $\textbf{x}$는 $\textbf{x}$인데 $\textbf{x}$ 주변에서의 아주 작은 $\textbf{x}$ 라는 뜻이다.
- 그러면 i 번째 턴에서의 $\textbf{x}^{*}_{i}$는
- 직전 턴에서의 (임시 최적값) $\textbf{x}^{\ast-}_{i-1}$에 (${}^{\ast-}$ 는 그 턴까지의 최적값을 의미)
- 이번 턴에서의 최적조금움직임값 $\delta\textbf{x}^{\ast}_{i}$ 를 더한 것이 된다.
- 즉 $\textbf{x}^{\ast}_{i}$ = $\textbf{x}^{\ast-}_{i-1}$ $+$ $\delta\textbf{x}^{\ast}_{i}$
- 이 때 저 최적조금움직임의 양이 너무 작거나 아니면 그냥 3번만 iteration 을 돌기로 했다던가 하는, 아무튼간의 엔지니어의 규칙에 도달하게 되면 $\textbf{x}^{\ast-}_{i}$ 를 최종최적값인 $\textbf{x}^{\ast}_{i}$ 이다 라고 땅땅 결정한다.
- 이 때 $\delta\textbf{x}^{\ast}$ 를 구하는 것은 다행히 closed form 으로 편하게 이루어진다.
- 우리는 앞서 $\textbf{A}\textbf{x} = \textbf{b}$ 라는 문제를 $\textbf{A}(\textbf{x} + \delta \textbf{x}) = \textbf{b}$ 라는 문제를 푸는 것 으로 변환한다.
- 여기에서 $\textbf{x}$는 직전 턴의 값이니 상수이고, $ \delta \textbf{x}$만이 변수임을 명심!
- 그러면 다시 변수만을 남기면, 이 문제는 $\textbf{C} \cdot \delta \textbf{x} = \textbf{d}$ 라는 문제로 치환된다 ($\cdot$는 (앞에서는 쓰는 것을 생략했지만) 단순한 매트릭스-벡터 곱 연산을 의미).
- 이 때 양변에 transposed C를 곱해주면 $\textbf{C}^T \cdot \textbf{C} \cdot dx = \textbf{C}^T \cdot \textbf{d}$ 이고,
- 이걸 넘겨주면 $\delta \textbf{x}^{\ast} = (\textbf{C}^T \textbf{C})^{-1} \textbf{C}^{T} \textbf{d} $ 가 된다. 이를 선형대수학용어로 ‘normal equation’을 푼다, 라고 말하기도 한다.
- 그럼 다시 약간 앞으로 돌아가서,
- $\textbf{A}\textbf{x} = \textbf{b}$ 나 $\textbf{C} \cdot \delta \textbf{x} = \textbf{d}$ 나 사실 완전히 동일한 모양새이다.
- 그런데 왜 $\textbf{x}$에 대해서는 normal equatoin 을 통해 $\textbf{x}^{\ast}$ 를 바로 계산하면 (하려면 테크니컬리 당연히 할수야 있지만) 논리적으로 말이 안되고,
- 왜 $\delta \textbf{x}$에 대해서는 normal equation 을 통해서 $\delta \textbf{x}^{\ast}$를 계산하면 말이 될까?
- 그것은 normal equation 을 Vector space 에 대해서만 적용할 수 있기 때문이다.
- 만약에 x의 성분에 수학적으로 vector space 가 아닌 요소들의 값이 단순히 나열되어서 들어있다면, 애초에 논리적으로 틀린 이야기가 된다는 뜻이다.
- 로보틱스에서 이러한 non-vector space인 요소는 rotation 이 대표적이다.
- 예를 들어, 앞서 x = (로봇의 위치, 로봇의 자세, 로봇이 느끼는 온도) 라고 했을 때, 로봇의 자세 (attitude)를 3x3 matrix 로 표현했다고 하자 (즉, SO(3)). 이 행렬의 값 9개를 x에 잘 펴서 나열해서 넣으면 될까? 물론 되기는 된다. 하지만 $\textbf{A}\textbf{x} = \textbf{b}$ 를 풀 때, normal equation 을 $\textbf{x}$에 대해서 바로 풀어버리면 그 때 나오는 $\textbf{x}^{\ast}$ 중 자세 부분의 9개 값은 논리적으로 그냥 말이 안된다는 것이다.
- 다시 강조: 최적화를 당하는 x 는 vector space 에 살고 있어야 한다!
- 단순히 프로그래밍에서 말하는 그냥 array (e.g., std::vector)를 말하는게 아니라 수학에서 말하는 vector space 여야한다는 뜻.
- 그래서 우리는 SO(3) 형태로 즐겨사용하는 rotation을 vector space 에 살고 있는 형태로 바꾸어 주어야 한다.
Rotation 최적화의 본질 preview: Optimization not on Lie group, but on Lie algebra
- 3x3형태의 흔히 사용하는 SO(3) rotation을 Lie group이라고 한다. Lie group은 manifold 라고 불리기도 한다.
- 어떤 SO(3) rotation 의 (identity 주변에서의) tangent space 에 살고 있는 아이들을 Lie algebra 라고 한다.
- 산수적으로,
- 어떤 3차원 vector (3요소 array) 가 있으면 그것에 cross operator를 취한 3x3 matrix 가 Lie algebra 이다.
- ps. cross operator 는 hat operator 라고도 불린다. Quaternion kinematics for the error-state KF 의 7쪽 아래 참고.
- 따라서 우리는 Lie algebra는 3-dim vector 와 동형(isomorphic)이다라고 이야기한다. 그게 그거다 라고 이해하면 되겠다.
- 비록 Lie algebra 는 3x3 matrix 의 형태를 가지고 있지만 사실상 3개의 값 (3-dof) 으로부터 생성되는 것이기 때문 이다. 따라서 사실상 Lie algebra 의 본질은 3개의 요소를 가지는 vector (3-dim array) 이다.
- 어떤 3차원 vector (3요소 array) 가 있으면 그것에 cross operator를 취한 3x3 matrix 가 Lie algebra 이다.
- 이 때, 이 tangent space (Lie algebra) 는 vector space이다.
- 산수적으로,
- Recap: optimization은 vector space 에서 수행되어야 한다.
- 즉, 우리는 위에서 서술한 iterative 한 방법을 (== Gauss-Newton with normal equation) 을 Lie group (SO(3))이 아닌 Lie algebra 에 살고있는 원소에 대해서만 적용할 수 있다.
- 그곳만이 vector space이기 때문이다. 어떤 논문들에서는 Euclidean space 라고 부르기도 한다.
- (편의상 $\textbf{x}$에 rotation만 있다고 하면)
- SO(3)는 이른 바 $\textbf{x}$이고, Lie algebra 의 최적값은 앞서 이야기했던 $\delta \textbf{x}^{*}$ 인것이다.
- $\textbf{x}$ 가 속한 공간은 꼭 vector space 일 필요는 없고 (어떤 group이어서 연산에 닫혀있기만 하면 되고)
- $\delta \textbf{x}$ 가 사는 공간은 꼭 vector space 여야 한다는 뜻.
- 왜냐하면 최적화는 vector space 에서만 수행될 수 있기 때문.
- 아직 이 말이 이해가 안가더라도 계속 읽어보자.
- 혹은 (명확한 notation에 비해 좋아하지 않지만) 굳이 비유를 들어보자면 …
- 기묘한 이야기에 나오는 upside down 같은거랄까…? 두 공간 사이에는 bijective map 이 존재한다.. 지하공간에서만 악마를 처치할 수 있다. 그리고 다시 지상공간으로 올라와야 한다… (
이 스토리가 맞던가?!)
- 기묘한 이야기에 나오는 upside down 같은거랄까…? 두 공간 사이에는 bijective map 이 존재한다.. 지하공간에서만 악마를 처치할 수 있다. 그리고 다시 지상공간으로 올라와야 한다… (
- SO(3)는 이른 바 $\textbf{x}$이고, Lie algebra 의 최적값은 앞서 이야기했던 $\delta \textbf{x}^{*}$ 인것이다.
Rotation 최적화의 본질: lift-solve-retract
- Recap: 그렇다면 $i$번째 turn의 최적 SO(3) 값은 $\textbf{x}^{\ast}_{i}$ = $\textbf{x}^{\ast-}_{i-1}$ $+$ $\delta\textbf{x}^{\ast}_{i}$ 가 되는 것이다.
- 그런데 이번에 주의해야할 것은 방금 식에서 $+$ 라는 상당히 일반적인 기호가 쓰였는데 저렇게 나이브하게 생각하면 안된다는 것이다.
- 왜냐하면 $\textbf{x}^{\ast-}_{i-1}$ (는 SO(3)) 와 $\delta\textbf{x}^{\ast}_{i}$ (는 SO(3)가 아님) 는 다른 공간에 살고 있기 때문이다.
- 서로 다른 공간에 살고 있는 두 원소 사이에 연산을 해줄 수는 없는 노릇이다.
- 따라서 이 때 해법은 Lie algebra 에 살고있는 $\delta\textbf{x}^{\ast}_{i}$ 를 Lie group (==SO(3)) 으로 변환해주면 된다.
- 그렇다면 그 이후에는 통상적인 matrix multiplication을 통해 두 rotation을 compose 해주면 된다.
- 근데 어떻게 변환하는가? 그것에 관한이야기가 이제 the exponential map, the logarithm map 이런 기술들이다.
- 이에 대한 자세한 내용은 A micro lie theory 의 Example 4 부분을 참고.
- 알고나면 그냥 간단한 matrix exponential 기법이며 수학이 아니라 사실상의 산수에 가깝다 (==계산기).
- ps. 대학교 저학년 입장에서 선형대수학 트릭들에 익숙하지 않다면 matrix 를 어떻게 exp하지? 라는 겁먹음이 바로 들수도 있겠으나, 사실상 exp 를 테일러급수로 펼쳐서 matrix 의 제곱들의 linear combination 모양으로 변환하는 것이므로 전혀 어려울 것이 없다. 이 때 내가 계산하기 귀찮고 어렵다고 어려운 것이 아니다. 계산은 어짜피 컴퓨터가 하는 것.
- 약간 설명이 장황했는데 정리해보자.
- Rotation 최적화를 한줄요약하자면
lift-solve-retract이다. - 이 말은 내가 지어낸 말은 아니고 아래 논문에서 이미 잘 정리되어있는 용어이다.
Absil, P-A., Christopher G. Baker, and Kyle A. Gallivan. "Trust-region methods on Riemannian manifolds." Foundations of Computational Mathematics 7 (2007): 303-330.- 2023년 12월 기준 인용 500회 정도 된다.
- SLAM 업계에서 유명한 논문인 IMU Preintegration on Manifold for Efficient Visual-Inertial Maximum-a-Posteriori Estimation (RSS 2015) 논문에서도 그런 말이 있다.

- 저 말이 내 말인데 …
- 좀 더 정리해서 표현하기 위해 GPT4에게 요약을 부탁하자.
- Rotation 최적화를 한줄요약하자면
-
요약:
이 글에서 언급된 ‘lifting’과 ‘retraction’은 다양체(manifold) 상에서의 최적화 문제를 처리하는 방법과 관련이 있습니다. 다양체 (e.g., SO(3))는 일반적인 유클리드 공간(Euclidean space)과 달리 비선형적인 구조를 가지고 있기 때문에, 이러한 공간에서의 최적화는 특별한 접근 방식이 필요합니다. ‘Lifting’과 ‘retraction’은 이러한 접근 방식의 일부입니다.
-
Lifting (리프팅): Lifting은 다양체 (e.g., SO(3)) 상의 점 주변에서의 최적화 문제를 해당 점에서의 접공간(tangent space) (e.g., Lie algebra)으로 “끌어올리는” 과정을 말합니다. 접공간은 해당 점 근처에서 다양체를 국소적으로 근사하는 유클리드 공간으로 볼 수 있습니다. Lifting은 원래의 비선형 문제를 접공간에서의 선형 또는 선형에 가까운 문제로 변환하여, 표준적인 최적화 기법을 적용할 수 있게 합니다.
-
Retraction (리트랙션): Retraction은 접공간에서 얻은 해를 원래의 다양체로 “되돌리는” 과정을 말합니다. 구체적으로, 리트랙션은 접공간의 원소(벡터)를 다양체 상의 점으로 매핑하는 함수입니다. 이 과정은 접공간에서의 최적화 결과를 다양체 상의 유효한 해로 변환합니다.
이러한 접근 방식의 예로 가우스-뉴턴(Gauss-Newton) 방법을 적용할 수 있습니다. 다양체 상에서의 최적화 문제를 접공간으로 “리프팅”하고, 이 공간에서 표준 최적화 방법을 적용한 다음, 그 결과를 “리트랙션”을 통해 다시 다양체로 되돌립니다. 이렇게 함으로써, 복잡한 비선형 다양체 상의 문제를 보다 쉽게 해결할 수 있습니다.
이러한 방법은 특히 로봇 공학, 컴퓨터 비전, 기계 학습 등에서 다양체 상의 데이터나 모델을 다룰 때 중요한 역할을 합니다. 예를 들어, 카메라의 움직임을 추적하거나 3D 형태를 복원하는 문제에서 이러한 방법들이 사용됩니다.
-
- 첨언
- Manifold (SO(3)) 에서 tangent space (Lie algebra) 로 가는 걸 끌어올리는 것으로 표현하고 있다. 매니폴드를 볼록한 원(circle)의 면, 그리고 tangent space 를 그 원의 볼록한 지점에서의 접평명이라고 시각적으로 생각해본다면, 끌어올린다는 표현이 납득이 된다.
- 반대로, Lie algebra (tangent space) 에서 Lie group (manifold) 로 돌아가는 건, (시각적으로 편의상) 내려가는 것이므로, retract (== draw back) 라고 표현했다.
- Trust-region methods on Riemannian manifolds 논문의 Figure 1 을 보면 왜 그런 표현을 썼는지 이해가 쉽게 된다.
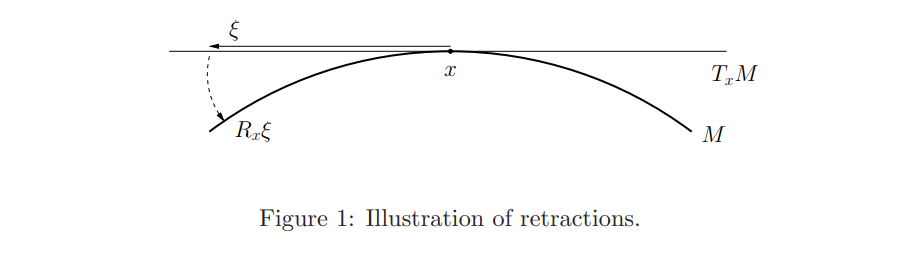
- Manifold (SO(3)) 에서 tangent space (Lie algebra) 로 가는 걸 끌어올리는 것으로 표현하고 있다. 매니폴드를 볼록한 원(circle)의 면, 그리고 tangent space 를 그 원의 볼록한 지점에서의 접평명이라고 시각적으로 생각해본다면, 끌어올린다는 표현이 납득이 된다.
- 결론: Rotation 최적화를 한줄요약하자면
lift-solve-retract이다.
Rotation 최적화: 요약
- 그러면 요약해보자.
- vector space 의 요소에 대해서 $\textbf{x}^{\ast}_{i}$ = $\textbf{x}^{\ast-}_{i-1}$ $+$ $\delta\textbf{x}^{\ast}_{i}$ 이렇게 썼던 것이
- 사실은 rotation (Lie group) 에 대해서는 $\textbf{x}^{\ast}_{i}$ = $\textbf{x}^{\ast-}_{i-1}$ $\cdot \textbf{Exp}$ $(\delta\textbf{x}^{\ast}_{i})$ 이렇게 써야 엄밀하게 맞는것이다.
- $ \delta\textbf{x}^{\ast}_{i} $ 가 Lie algebra 에 살고있으니 $\textbf{Exp}(\cdot)$을 통해서 그걸
Retract해서 Lie group으로 가져온 다음에야, 동일한 공간에 살고있는 두 원소끼리의 연산 (i.e., matrix multiplication) 을 먹여줄 수 있는 것이다. - 그런데 매번 저렇게 쓰자니 좀 귀찮고 예쁘지도 않다. 왜냐하면 (Lie group에 대해 잘 알고있는 사람이 독자라면) 좀 더 추상적인 개념적으로는 같은 공간에 살든말든 아무튼 기존 값에 미소최적범위를 더해주었다 라는 사실은 변하지 않기 때문이다.
- 따라서 어떤 책이나 논문들에서는 $\textbf{x}^{\ast}_{i}$ = $\textbf{x}^{\ast-}_{i-1}$ $\oplus$ $\delta\textbf{x}^{\ast}_{i}$ 라던가
- $\textbf{x}^{\ast}_{i}$ = $\textbf{x}^{\ast-}_{i-1}$ $\boxplus$ $\delta\textbf{x}^{\ast}_{i}$ 이런식으로 +에 box 나 O 를 둘러서 표현하기도 한다 (boxplus, oplus 라고 읽음).
- ps. 그리고 엄엄밀하게 $\textbf{Exp}$라는 연산자는 존재하지 않는다 (소문자인 $\textbf{exp}$ 만 존재).
- 따라서 사실은 $\textbf{exp}({\delta \textbf{x}_{i}}^{\wedge})$ 이렇게 써야 맞는 것이다 (이 때 ${}^{\wedge}$ 는 hat operator. 3-dim vector를 skew symmetric matrix로 만든다). 그런데 그러면 쓰는게 너무 귀찮고 안이쁘니 e를 대문자 E로 바꾸어서 쓰고 ${}^{\wedge}$를 굳이 적지않더라도, 저걸 의미하는 것임을 잘 알아들으렴ㅋ 라고 약속하고 있다.
- $ \delta\textbf{x}^{\ast}_{i} $ 가 Lie algebra 에 살고있으니 $\textbf{Exp}(\cdot)$을 통해서 그걸
- 방금 한 얘기에서 핵심을 요약해보자.
- 흔히 쓰는 SO(3) 형태의 rotation은 vector space 에 살지 않는다.
- 따라서 iterative optimization (e.g., Gauss-newton) 을 바로 적용할 수 없다. 따라서 SO(3)를 Lie algebra라는 (원래 공간과 bijective한) vector space 에서의 표현법으로 옮겨 갈 필요가 있다. ==
Lift - vector space와 동형인 Lie algebra 공간에서 최적화 를 진행한다 (e.g., solve the normal equation: $\delta \textbf{x}^{\ast} = (\textbf{C}^T \textbf{C})^{-1} \textbf{C}^{T} \textbf{d} $) ==
Solve - 그 최적값을 원래의 SO(3) 공간으로 가져온 다음 기존 값에 미소최적값을 더해서 이번 턴의 최적 SO(3) 값을 생성 (i.e., $\textbf{x}^{\ast}_{i}$ = $\textbf{x}^{\ast-}_{i-1}$ $\oplus$ $\delta\textbf{x}^{\ast}_{i}$) 한다. ==
Retract
Rotation 최적화: Notations, and Terminologies
- group 이니 algebra이니 하는 수학적인 개념을 떠나서라도, 아무튼 rotation의 parametrization 이 여러 종류가 있다 라는 사실을 알게되었다.
- 그래서 rotation parametrization 에 대해서 공부하는 것이 중요하다.
- 이는 지금까지 이야기했듯이 일단 최적화 관점에서 중요하다.
- 그리고 그 외에도 quaternion 과 같은 또 다른 표현법도 존재한다. quaternion은 SO(3)보다 간결한 표현 (4개의 숫자만 필요) 으로 global orientation 을 표현하는 데 유용하다는 장점이 있다.
- Terminologies: Lie algebra (3-dim array에 hat 연산이 취해진 3x3 matrix) 의 본체인 the 3-dim array 를 rotation parametrization 관점에서
- 어떤 책들은 angle-axis representation, rotation vector 이런식으로 부르기도 한다.
- 즐겨 쓰는 scipy 의 rotation library 에서도 이를 부를 때
rotvec이라고 칭하고 있다.
- 즐겨 쓰는 scipy 의 rotation library 에서도 이를 부를 때
- 혹은 state estimation 책/논문들에서는 SO(3)의 error-state 이다~ 라고 부르기도 한다.
- Lie algebra (SO(3)의 tangent space) 의 요소를 계속 $\delta \textbf{x}$ 와 같이 표기해왔던 것을 떠올려보자. 그리고 그것의 물리적인 의미는 미소변위를 얼마만큼 최적으로 조절해야 전체적인 관점(==원래 공간)에서도 최적값에 더 가까워질까, 를 의미하므로 <
정답지에서 약간 아직은 어느정도 떨어져있는 작은 에러> 혹은 <그걸 극복하기 위해 보상해주어야 하는 미소 변위> 라는 의미에서error-state라는 용어가 쓰이고 있구나 라고 이해하면 되겠다.
- Lie algebra (SO(3)의 tangent space) 의 요소를 계속 $\delta \textbf{x}$ 와 같이 표기해왔던 것을 떠올려보자. 그리고 그것의 물리적인 의미는 미소변위를 얼마만큼 최적으로 조절해야 전체적인 관점(==원래 공간)에서도 최적값에 더 가까워질까, 를 의미하므로 <
- 어떤 책들은 angle-axis representation, rotation vector 이런식으로 부르기도 한다.
Nano Lie Theory: Beyond the Basics
- 기본을 넘어 1
- 여기까지가 A micro Lie theory for state estimation in robotics 의 II-E 까지의 내용이다.
- 이제 남은 것 (II-F,G,H,I) 은 adjoint, 미분, covariance propagatoin, 적분 정도이다.
- rotation parametrization 에 대해 처음 접할 때의 두려움은 책마다 다른 용어들, Lie algebra 에 대한 갑작스러운 정의부터 버억 하면서 나오는 점, 그리고 그것이 왜 필요한지 납득시키지 않고 시작하는 점, 이라고 생각하는데 이런 우려들에 대해 이 Nano Lie theory 에서 정리가 되었으리라 생각한다.
- 그러면 남은 derivatives on Lie groups, Discrete integration on manifolds 등은 좀 더 쉽게 각자 읽을 수 있을 것이다.
- 따라서 남은 것들에 대한 설명은 생략한다!
- 기본을 넘어 2
- 그런데 $\textbf{x}^{\ast}_{i}$ = $\textbf{x}^{\ast-}_{i-1}$ $\oplus$ $\delta\textbf{x}^{\ast}_{i}$ 처럼 왜 $\delta\textbf{x}^{\ast}_{i}$를 계속 $\textbf{x}^{\ast-}_{i-1}$ 의 오른쪽에만 쓸까?
- $\oplus$ 는 교환법칙이 성립하지 않기 때문에 왼쪽에 연산해주는 것과 오른쪽에 연산하는 것은 분명히 다르다.
- 그러면 어떻게 다를까? 이에 대해서는 Quaternion kinematics for the error-state KF의 section 4.4.1 및 4.4.2 를 참고바람.
- 한줄요약하자면 local coordinate에서 바라본 조금 을 더해줄 거냐, world coordinate에서 바라본 조금 을 더해줄거냐 라는 의미차이가 있다.
추천 읽기자료
- 2018, A micro Lie theory for state estimation in robotics
- 2017, Quaternion kinematics for the error-state Kalman filter
- 2015, IMU Preintegration on Manifold for Efficient Visual-Inertial Maximum-a-Posteriori Estimation
- 훌륭한 시각화 자료 - https://thenumb.at/Exponential-Rotations
Next work
- C++ library들을 통해 Lie group 및 Lie algebra 의 여러 연산들에 대해 실습해보자 (A nano Lie theory: 2편 (실습 편)).
