Single Rotation Averaging 을 구현해보자

• 어렵지 않아요
• $\text{SO(3)}$ 와 $\mathfrak{so(3)}$ 미분 고수되는 법

개요

• Rotation averaging 은 SfM (Structure-from-motion), SLAM 등에서 자주 등장하는 task 이다.
  • ps. rotation averaging 이 무엇인지에 대해서는 다음 논문을 참고.
    • Rotation Averaging by Richard Hartley, et al.
    • 이 논문을 인용한 논문들 중 인용수가 많은 것을 보는 것 또한 도움이 되겠다.
• 왜 필요한가?
  • 대부분의 geometric computer vision 문제에서, residual 을 최소화 할 때,
  • 현재 solution으로부터 delta 만큼 조금씩 이동해나가면서 최종 solution 으로 수렴해나가는데 (i.e., Gauss-Newton),
  • 이 작업은 vector space 에서만 가능하므로,
  • nonlinear 한 term 들을 국소적으로 linearization 해주어야 하는데,
    • 이 이야기에 대한 더 자세한 설명은 예전 포스트 를 참고.
  • 이 때, 직전 solution 이 안 좋다면 (== global solution 으로부터 멀다면)
  • 해가 수렴하기 어렵다.
  • 이것이 SfM or SLAM 에서 더욱 문제가 되는 건,
  • N 개의 노드 (수십개일수도, 수천 수만 개 일수도) 의 pose 를 모두 joint 하게 최적화 하는 문제를 푸는 것이 SfM or SLAM 인데
  • rotation 이 nonlinear 한 요소이고,
  • Gauss-newton 과정에서, rotation 부분의 current solution 이 안좋다면 이는 pose 중 rotation 이 아니라 position 부분에도 악영향을 끼칠 수 있기 때문이다 (그리고 마찬가지로 그러한 한 노드의 에러가 다른 노드들에도 악영향을 끼칠 수도 있겠다).
• 그래서, 특히 nonlinear 한 term인 rotation 부분을 global solution에 잘 맞게 초기값을 잘 설정해둘 수 있다면, translation loss 등은 또한 쉽게 풀릴 수 있을 것이다.
• 예를 들어서, 하나의 노드 (pose) 의 rotation (attitude) 에 대한 measurement 가 k 개 있을 때, 이것을 수만개 노드의 joint optimization 을 풀 때 모두 constraint 로 넣어주는 것이 아니라, k 개의 measurement 들을 잘 분석해서 신뢰할만한 하나의 값만을 도출한 다음, 그것만을 전체 최적화 문제의 constraint 로 추가해줄 수 있겠다.
• 즉, single rotation averaging 이라는 task는,
  • 하나의 노드 (pose) 의 rotation (attitude) 에 대한 measurement 가 k 개 있을 때,
  • 이 측정치들을 모두 적당히 만족하도록 고려했을 때,
  • 그 노드의 rotation (attitude or orientation 등으로도 불림) 은 그래서 최종적으로 무엇인가, 에 대한 대답을 하는 문제이다.
• rotation (i.e., SO(3)) 은 vector space 에 살고 있지 않기 때문에, 단순히 xyz 들을 k 로 나누는, 즉, $ \textbf{sum}(\textbf{R}_1, \textbf{R}_2, \textbf{R}_3) / 3$ 과 같이 나이브하게 계산할 수는 없다.
• 물론 sum 이라는 함수와 / 라는 나눗셈을 어떻게 정의할거냐에 달린것이긴 하지만… 여기에서 이야기하려고 하는 것은 저런 deterministic 한 계산을 한 방에 하려는 것이 아니라, 대신에 iteratively 조정해나가는 과정을 어떻게 수행할 수 있느냐? 하는 점이다. 즉, 저 평균조차도 iterative 하게 얻어져야 한다는 것이다. 이는 다시 말하지만 rotation 이 살고 있는 공간은 nonlinear 하고 국소적으로 (== iterative optimization 이 수행되는 tangent space) 만 vector space 이기 때문에 저런 일반 연산을 수행할 수 있기 때문이다.
• 위 논문 Rotation Averaging by Richard Hartley, et al. 에서는 rotation definition을 먼저 하고, 유용한 성질들에 대해 이야기 한 뒤, 여러 distance 에 대해서도 논의하고, 메인에서는 1. single rotation averaging 과 2. multiple rotation averaging 에 대해 이야기한다.
• 그 중, 이 포스트에서는 1. single rotation averaging 에 대해서만 알아볼 것이다.
  • rotation 의 정의나 기본적인 성질에 대해서는 독자가 알고있다고 가정한다.
  • 그나저나 2. multiple rotation averaging 는 rotation only pose-graph optimization 이라고도 불린다.
• 그리고 위 논문을 보면 rotation 이 살고있는 공간에서 distance 를 정의하는 방식이 여러 개가 있음을 알 수 있는데, 본 포스트에서는 가장 기본적이고 정석적인 tangent space 에서의 L2 loss 로 정의할 것이다. 그리고 그 차이를 iteratively 줄여나가면, 원래 rotation 공간 (we call it manifold, SO(3)) 에서도 최적화가 되어있는지 보일 것이다.

티저

• 이 포스트에서는, single rotation averaging 을 from scratch 로 구현해보고 실습해보자.
• 티저
  • 결과부터 먼저 보이자면 아래 그림과 같다.
    • 설명
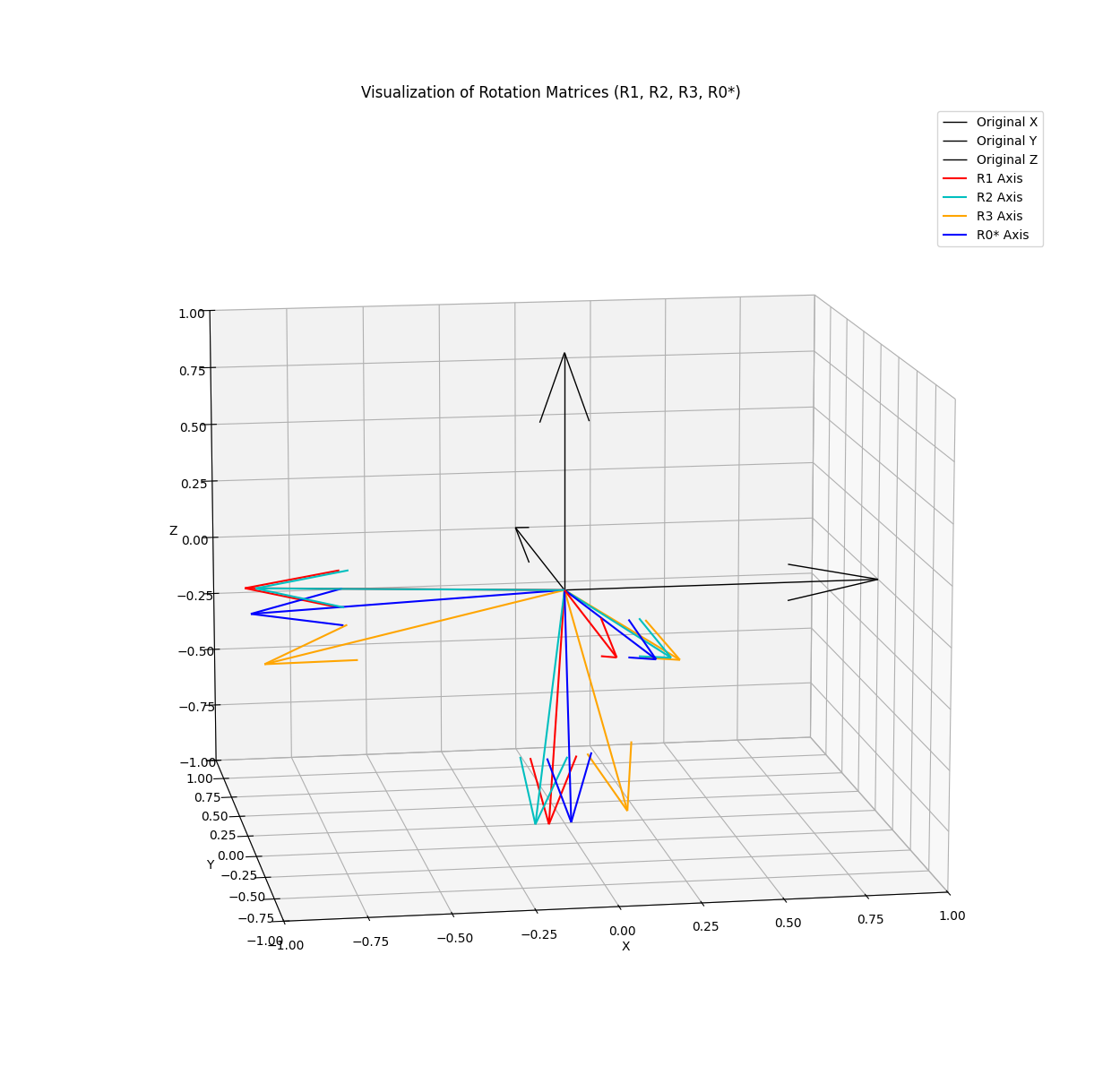
      • 빨강, 청록, 노랑 axes 들은, 어떤 로봇의 어떤 시점에서의 대한 자세 (rotation, attitude, orientation 등으로 불림) 예측 값을 의미한다.
        • 예를 들어서 동일한 센서로 세 번 측정했는데, 현실세계의 센서란 noisy 하고 불완전하므로 조금씩 저렇게 다른 결과가 나올 수 있겠다.
      • 그러면 저 셋 정보를 모두 만족하는 (== 개념적으로 평균, 실제 계산은 iterative optimization) 값을 구해서, 로봇의 자세는 이것이야! 라고 말해야 할텐데,
      • 그 결과는 파랑색 축이다.
      • 일단 사람이 시각적으로 보았을 때 말이 맞는 것 같아보인다. 파랑이 세 축 모두에서, 다른 셋 들의 중간 즈음에 위치하는 것을 잘 볼 수 있다.
    • 어떻게 구현했는지 이제 차차 설명을 해보자.

  

배경지식 1

• 일단 iterative optimization 의 기계적인 과정은 아래와 같다 (이걸 나는 개인적으로 ‘기계적인 과정’ 이라던가, ‘산수’ 라던가, ‘계산기’라고 부른다. 즉, 어렵지 않다는 말이다).
  • 이 그림은 매번 추천하는 자료인, ICRA 2016 SLAM tutorial 중, Giorgio Grisetti 교수님 슬라이드 에서 가져온 것이다.

  

• 여기서 $\textbf{J}$ 만 구하면 된다.
  • ps. 내가 다루는 1. 센서 특성 (예: 카메라는 pixel 로 구성되어있고 세상의 정보가 projective 하게 생성된다) 과, 2. 그 센서 특성을 고려한 observation model (residual model) (예: 그러므로 pose 가 true였다면 projection 했을 때의 reprojection error 가 작을 것이다. 그것은 (u, v) 공간에서의 그저 두 차원 벡터의 뺄셈으로 정의된다), 이 두 가지를 어떻게 잘 알고 잘 다루고 잘 구현할 수 있느냐가 단순히 geometric vision 전공자를 넘어서서 SLAM engineer의 도메인 놀리지라고 할 수 있겠다.
  • J가 어떻게 구해지느냐만 다르지, 그 이후과정은 모든 논문들이 동일하다.

배경지식 2

• $\textbf{J}$ …
• 자코비안, 야코비안, … 다양하게 불리는 이 녀석
  • 그냥 multi-dimensional 기울기라고 생각하면 된다.
  • Gauss-Newton optimization 을 하기 위해서는 기울기 값을 알아야 하기 때문.
  • 예전 포스트 에서도 이 얘기는 이미 했었다 (사실 결국 맨날 이 얘기를 하게 되는 것이다 …).
    • 여기서도 다시 말하자면, 자코비안은 이렇게 기억하면 된다. matrix 네모의 세로(즉, row 들) 는 cost, 가로(즉, column들)는 state.
• 아무튼 본 포스트에서도 결국, 어떤 residual function에 대한, 최적 rotation 의 미소변화량, 의 미분 matrix (== 자코비안) 를 계산하는 것이 관건이 된다.
• rotation 에 대해 해보자.

유도 과정 (Derivation)

• iterative 하게 an averaged rotation 값을 예측할 것이므로,
• 현재 ($t$ 번째 step) 까지 예측된 값을 $\textbf{R}^{(t)}$ 이라고 해보자.
  • == 위의 티저 그림에서 파랑 화살표 (혹은 이것에 도달하기 전의 스텝)
• 그리고 어떤 measurement $\textbf{R}_1$, $\textbf{R}_2$, $\textbf{R}_3$ 이렇게 3개가 있었다고 하자.
  • == 위의 티저 그림에서 파랑을 제외한 나머지 화살표들
• 그러면, 이 세 개의 measurement 로부터 각각 $\textbf{H}_i$ 와 $\textbf{e}_i$ 가 생성되고,
• 전체 $\textbf{H}$ 와 $\textbf{b}$ 는 앞서 소개한 tutorial slide 에서 설명한대로 (단순한 덧셈으로!) 얻어지게 된다.
  • 코드로도 당연히 너무 간단하다.

      H += J_i.T @ J_i 
      b += J_i.T @ e_i 
    

• 그럼 우리가 지금 유도하려는 것은 결국 저 J_i 와 e_i 가 무엇인가 하는 것이다.
• J_i 는 e_i를 미분함으로써 얻어지는 것이므로, 먼저 e_i 를 정의해야 한다.
• e_i는 다음과 같다.
  • 우리는 iteratively gauss newton optimization 을 수행할 것이므로
  • 그 최적조금움직임 해는 rotation 의 tangent space 에서만 정의가 가능하다. 거기만이 vector space이기 때문이다.
    • 이 말이 이해가 가지 않는다면 예전 포스트를 읽고 오기를 추천한다. 예전 포스트1 와 예전 포스트2.
  • 원래의 rotation 공간인 $\mathrm{SO(3)}$ 에서의 residual (은 3 by 3 matrix 이다) 에 $\textbf{Log}(\cdot)$ 연산을 취해주면 3-dim vector가 생성된다.
  • 그것이 우리의 e_i가 된다.
  • 왜 그렇게 하냐고 묻는다면, 다시 요약하자면, Gauss-Newton opt 는 vector space 에서만 수행할 수 있는데, 그것은 $\mathrm{SO(3)}$ 의 tangent space인 $\mathfrak{so(3)}$ 에서 정의된다고 할 수 있다. 그래서 우리는 $\mathrm{SO(3)}$ 에서 distance 를 구하고, 거기에 $\textbf{Log}(\cdot)$ 연산을 취해서, $\mathfrak{so(3)}$ 상에서의 distance 를 정의했다고 할 수 있다.
    • ps. 왜 $\textbf{Log}(\cdot)$ 연산을 취해야, $\mathfrak{so(3)}$ 상에서의 distance 가 되는지에 대해서는 여기에서 더 설명하지는 않는다. 그것은 약간 기본이기 때문… 여기서부터는 Quaternion kinematics for the error-state Kalman filter 이나, 아니면 다른 논문들을 참고 바람.
  • 그리고 $\textbf{Log}(\cdot)$ 는 사실 $\textbf{log}(\cdot)$ 라는 연산에 unskew 를 해주는 과정을 더한 것을, 간단하게 문자로 표현하려고 l을 L로만 바꿔쓴것이다.
• 그럼 이제까지 tangent space 상에서의 error function (our observation model) 을 정의했으니, 이것의 Jacobian을 구해보자.
• 먼저, e_i의 수식을 코드가 아니라 latex으로 다시 적어보자.
  • $e_i = \textbf{Log}(error(\mathbf{R}))$ 이고, 여기서 $error(\mathbf{R})$는 다음과 같이 정의된다. $error(\mathbf{R}) = \mathbf{R}_{\text{measurement}} \ominus \mathbf{R}_{\text{estimated}} = \mathbf{R}_{\text{estimated}}^\top \cdot \mathbf{R}_{\text{measurement}}$
    • 왜 transpose 의 왼쪽곱이 되는지 까지 여기서 설명하지는 않는다..
• 앞서 우리의 measurement 를 간단히 $\mathbf{R}_{i}$ 라 불렀고 (예: $\mathbf{R}_{1}$, $\mathbf{R}_{2}$, $\mathbf{R}_{3}$), 우리의 (step $t$에서의) 예측값을 $\mathbf{R}^{(t)}$라고 불렀으니, 다시 식을 써보면
• $e_i = \textbf{Log}({\mathbf{R}^{(t)}}^\top \cdot \mathbf{R}_{i})$ 라고 할 수 있다.
• 이제 $\mathbf{J}_i$를 논할 수 있다.
• $\mathbf{J}_i$는, 우리의 관심사(최적조금움직임값이 얼마인지)인 tangent space 에서의 value (rotation vector 라고 하자) 인, 이 3-dim vector인 이 값이 조금 움직일 때, 위의 $e_i$가 얼마나 변하는지? 로 정의된다.
• 그 최적으로 조금 움직인 rotation vector 를 $\delta \boldsymbol{\theta}$라고 하면, (ps. 조금이라는 의미에서 $\delta$ 를 붙임)
• 이 때 (== step $t$에서 조금만 최적으로 더 움직여 본)의, 예측 값은 ${(\mathbf{R}^{(t)} \oplus \delta\boldsymbol{\theta})}$ 가 되고,
• $e_i$는 따라서 $\textbf{Log}({(\mathbf{R}^{(t)} \oplus \delta\boldsymbol{\theta})}^\top \cdot \mathbf{R}_{i})$ 가 되며,
  • ps. 이 때 $\oplus$란 matmul 을 의미한다. 하지만 왜 그렇게 쓰나면, $\delta\boldsymbol{\theta}$ 는 vector 이고, rotation matrix 가 살고있는 SO(3) 에 살고있지 않기 때문에, 일반적인 더하기나 곱하기 (i.e., $\cdot$) 기호를 쓰면 논리가 맞지않게 되어 편의상 $\oplus$ 나 $\boxplus$와 같은 기호로 표기하는 풍습이 있다. 실제로는 oplus 가 적혀있다면, rotation vector 에 Exp를 취한 뒤 matmul 을 해준다 라고 이해하면 된다.
    • 이미 존재하는 다양한 공부자료들로 그 설명을 대신한다.
      • Integrating Generic Sensor Fusion Algorithms with Sound State Representations through Encapsulation of Manifolds
      • A tutorial on SE(3) transformation parameterizations and on-manifold optimization
      • Lie Theory for State Estimation in Robotics
• $J_i = \frac{\partial e_{i}(\delta \boldsymbol{\theta})}{\partial \delta\boldsymbol{\theta}} = \frac{\partial \textbf{Log}({(\mathbf{R}^{(t)} \oplus \delta\boldsymbol{\theta})}^\top \cdot \mathbf{R}_{i})}{\partial \delta\boldsymbol{\theta}}$ 가 된다.
• 이것이 실제로 코드상으로 어떻게 구현이 되는지, symforce 등에 맡겨도 되겠지만…
• 우리가 알고 있는 rotation 의 유용한 수식들을 잘 조합해서, 잘 풀어서 deterministic 하게 써내면 (== 코드로 옮기기 쉬운 형태) 우리의 목표 달성이다.
• 트릭 1
  • ${\mathbf{R}^{(t)} \oplus \delta\boldsymbol{\theta}}$ 은
  • $\mathbf{R}^{(t)} \cdot \textbf{Exp}(\delta\boldsymbol{\theta})$ 인데,
    • 여기서, $\delta\boldsymbol{\theta}$ 가 작은 값일 때는 (최적 ‘조금’움직임 값이므로 이렇게 가정할 수 있음)
    • $\textbf{Exp}(\delta\boldsymbol{\theta}) \sim \textbf{I} + [\delta\boldsymbol{\theta}]_{\times}$ 로 근사할 수 있다.
      • note: $[ … ]_{\times}$ 는 input이 3-dim vector이고, output이 skew symmetric matrix 인 함수를 의미한다.
  • 그러면 다시, $\mathbf{R}^{(t)} \cdot \textbf{Exp}(\delta\boldsymbol{\theta}) = \mathbf{R}^{(t)} \cdot (\textbf{I} + [\delta\boldsymbol{\theta}]_{\times})$ 가 된다.
• 그러면 $J_i = \frac{\partial \textbf{Log}({(\mathbf{R}^{(t)} \oplus \delta\boldsymbol{\theta})}^\top \cdot \mathbf{R}_{i})}{\partial \delta\boldsymbol{\theta}}$ 는
  • $J_i = \frac{\partial \textbf{Log}({ (\mathbf{R}^{(t)} \cdot (\textbf{I} + [\delta\boldsymbol{\theta}]_{\times})) }^\top \cdot \mathbf{R}_{i})}{\partial \delta\boldsymbol{\theta}}$ 와 같이 다시 쓸 수 있다.
• 트릭 2
  • $\textbf{Log}(\cdot)$ 연산자를 $\text{unskew}(\textbf{log}(\cdot))$ 이렇게 나눠서 쓸 수 있다. 여기서 unskew 라는 말은 그냥 편의상 내가 붙인 말이며 (좀 더 코드 친화적으로 설명하기 위해서), 실제로는 스큐시메트릭 행렬을 벡터로 다시 변환하는 연산을 “vee” 연산이라고 흔히 부른다. $\vee$ 기호로 쓴다.
  • 그러면 $J_i = \frac{\partial \texttt{vee}(\textbf{log}({ (\mathbf{R}^{(t)} \cdot (\textbf{I} + [\delta\boldsymbol{\theta}]_{\times})) }^\top \cdot \mathbf{R}_{i}))}{\partial \delta\boldsymbol{\theta}}$ 와 같이 다시 쓸 수 있다.
• 트릭 3
  • $(AB)^\top = B^\top \cdot A^\top$ 을 이용해서, $\textbf{log}(\cdot)$ 안의 식을 정리하면
  • $\left( \mathbf{R}^{(t)} \cdot (\mathbf{I} + [\delta\boldsymbol{\theta}]_\times) \right)^\top = (\mathbf{I} + [\delta\boldsymbol{\theta}]_\times)^\top \cdot (\mathbf{R}^{(t)})^\top$ 가 된다.
• 트릭 4
  • skew-symmetric matrix의 정의를 사용하면, $([\delta\boldsymbol{\theta}]_\times)^\top = -[\delta\boldsymbol{\theta}]_\times$ 이다.
  • 그리고 $(A + B)^\top = A^\top + B^\top$ 이므로
  • 위의 텀 $\left( \mathbf{R}^{(t)} \cdot (\mathbf{I} + [\delta\boldsymbol{\theta}]_\times) \right)^\top = (\mathbf{I} + [\delta\boldsymbol{\theta}]_\times)^\top \cdot (\mathbf{R}^{(t)})^\top$ 은 $ = (\mathbf{I} - [\delta\boldsymbol{\theta}]_\times) \cdot (\mathbf{R}^{(t)})^\top$ 가 된다.
  • 이제 그러면 residual 식은 $e_i(\delta\boldsymbol{\theta}) = \textbf{Log}\left( (\mathbf{I} - [\delta\boldsymbol{\theta}]_\times) \cdot (\mathbf{R}^{(t)})^\top \cdot \mathbf{R}_i \right)$ 가 된다.
• 트릭 5
  • 여기서 $\mathbf{E} = (\mathbf{R}^{(t)})^\top \cdot \mathbf{R}_i$ 라고 할 때,
  • 최적화 과정에서 현재 추정치 $\mathbf{R}^{(t)}$는 측정치 $\mathbf{R}_i$에 근접하므로 $\mathbf{E}$는 단위 행렬에 근접한다.
    • 즉, $\mathbf{E} \sim \mathbf{I}$ 라고 할 수 있다.
  • 따라서:
    • $e_i(\delta\boldsymbol{\theta}) = \textbf{Log}\left( (\mathbf{I} - [\delta\boldsymbol{\theta}]_\times) \cdot \mathbf{E} \right) = \texttt{vee}(\textbf{log}\left( (\mathbf{I} - [\delta\boldsymbol{\theta}]_\times) \cdot \mathbf{E} \right)) = \texttt{vee}(\textbf{log}\left( (\mathbf{I} - [\delta\boldsymbol{\theta}]_\times) \right))$ 로 근사할 수 있다.
• 트릭 5
  • 테일러 전개를 이용하자
  • $\textbf{log}(\mathbf{I} + \mathbf{A}) = \mathbf{A} - \frac{1}{2}\mathbf{A}^2 + \frac{1}{3}\mathbf{A}^3 - \cdots$ 이다.
  • 2차 항 이상은 작으므로 무시하면,
  • $\textbf{log}\left( (\mathbf{I} - [\delta\boldsymbol{\theta}]_\times) \right) \sim - [\delta\boldsymbol{\theta}]_\times$ 이다.
• 결론
  • 따라서 $J_i = \frac{\partial e_{i}(\delta \boldsymbol{\theta})}{\partial \delta\boldsymbol{\theta}} = \frac{\partial \textbf{Log}({(\mathbf{R}^{(t)} \oplus \delta\boldsymbol{\theta})}^\top \cdot \mathbf{R}_{i})}{\partial \delta\boldsymbol{\theta}} = \frac{\partial \texttt{vee}(\textbf{log}\left( (\mathbf{I} - [\delta\boldsymbol{\theta}]_\times) \right))}{\partial \delta\boldsymbol{\theta}} = \frac{\partial \texttt{vee}(- [\delta\boldsymbol{\theta}]_\times)}{\partial \delta\boldsymbol{\theta}} = \frac{\partial \texttt{unskew}(- \texttt{skew}(\delta\boldsymbol{\theta}))}{\partial \delta\boldsymbol{\theta}} = \frac{\partial (- \delta\boldsymbol{\theta})}{\partial \delta\boldsymbol{\theta}} = -\mathbf{I} $ 가 된다.
    • ps. $\texttt{vee}$ 와 $\texttt{unskew}$ 는 같은 표현이다. skew 작업을 역으로 해준다는 의미에서 코드에서는 unskew 라고 적는게 좀 더 이해가 쉬워서 그렇게 표현해보았다. 마찬가지로 $[\cdot ]_\times$ 라는 표현보다는 $\texttt{skew}$ 라고 적으면 좀 더 짝이 맞는 듯한 느낌이다 (코드 레벨에서 더 좋은 가독성 보유 가능).

구현

• 지금까지 e 와 J를 구했다.
• 따라서 코드레벨에서는 다음과 같다. 매우 간단하다.

    # Initialized at the first step's solution
    R_optimal = ... # e.g., = R1 
  
    # Gauss-newton update 
    for i in range(max_iters):
        H = np.zeros((3, 3))
        b = np.zeros(3)
          
        # gather measurements 
        for R_i in [R1, R2, R3]:
            e_i = unskew(log(np.dot(R_optimal.T, R_i))) 
            J_i = -1 * np.eye(3) 
  
            H += J_i.T @ J_i 
            b += J_i.T @ e_i 
          
        # solve the normal equation H * dtheta = -b 
        dtheta_optimal = np.linalg.solve(H, -b)
          
        # check termination condition (convergenceness)
        print(f"iter {i}: dtheta: {dtheta}")
        if np.linalg.norm(dtheta) < tolerance:
            print(f"The solution converged. terminate the GN opt at iteration {i}\n")
            break
          
        # update the solution 
        R_optimal = R_optimal @ Exp(dtheta_optimal)
  
        # (optional) 업데이트 한 SO(3) 가 정의를 만족하도록 강제 (make det = 1)
        U, _, Vt = np.linalg.svd(R0)
        R0 = np.dot(U, Vt)
        if np.linalg.det(R0) < 0:
            U[:, -1] *= -1
            R0 = np.dot(U, Vt)
  
  

결론

• 코드에서 마지막에 # update the solution 부분에서, tangent space에서 얻은 최적조금움직임 값을 원래 rotation에 첨가해주는 것을 “retract” operation 이라고 부른다. 전체 과정은 lift-solve-retract pipeline 이라고 불리기도 한다. 예전 포스트 에서 언급해두었음.
• 2016 T-RO Paper 인 On-Manifold Preintegration for Real-Time Visual-Inertial Odometry 의 본질도 사실 이것이 전부이며… 쫄 필요가 없겠다.
• 결론적으로 간단한 measurement 3개 짜리 rotation averaging 이라는 task를 직접 from-scratch 부터 구현해봄으로써, 결론적으로는 최신 visual inertial odometry 방법도 이론적으로는 같다는 이야기를 하고 싶었다.

실습

• 실습 코드는 여기 (main_onmanifold_ganussnewton.py) 에 있다. (디펜던시는 유명한 numpy 와 matplotlib 이므로 별도 도커환경 설정은 생략하고 실습해보자.)
• GN 최적화 과정에서 weight 를 고려한 update 예시를 구현해보자. 예를 들어서 3개의 measurement 중 하나를 특히 더 신뢰하고 싶다면?
  • 이를 더 확장하면 outlier robust rotation averaging 까지 실습해볼 수 있겠다. 심한 outlier 를 포함한, 100개의 measurement 인 경우로 확대해보자.